GEOMETRÍA CLÁSICA

GEOMETRÍA PROYECTIVA

 arco Maximal en un finito plano proyectivo es un más grande posible ( k , d ) - arco en ese plano proyectivo. Si el plano proyectivo finito tiene un orden q (hay q +1 puntos en cualquier línea), entonces, para un arco máximo, k , el número de puntos del arco es el máximo posible (= qd + d - q ) con el Propiedad que no hay d +1 puntos del arco en la misma línea.

Definición [ editar ]

Dejar $${\ displaystyle \ pi}Ser un plano finito proyectivo de orden q (no necesariamente desarguesiano ). Los arcos máximos de grado d (2 ≤ d ≤ q - 1) son ( k , d ) - arcos en$${\ displaystyle \ pi}, donde k es máximo con respecto al parámetro d , en otras palabras, k = qd + d - q .

De manera equivalente, se pueden definir arcos máximos de grado d en$${\ displaystyle \ pi}como conjuntos de puntos K no vacíos, de modo que cada línea intersecte el conjunto en puntos 0 o d .

Algunos autores permiten que el grado de arco máximo sea 1, qo incluso q + 1. ^[1] Dejando que K sea ​​un máximo ( k , d ) -arc en un plano proyectivo de orden q , si

• d = 1, K es un punto del plano,
• d = q , K es el complemento de una línea (un plano afín de orden q ), y
• d = q + 1, K es el plano proyectivo completo.

Todos estos casos se consideran ejemplos triviales de arcos máximos, que existen en cualquier tipo de plano proyectivo para cualquier valor de q . Cuando 2 ≤ d ≤ q - 1, el arco máximo se llama no trivial , y la definición dada anteriormente y las propiedades enumeradas a continuación se refieren a arcos máximos no triviales.

Propiedades [ editar ]

• El número de líneas a través de un punto fijo p , no en un arco máximo K , intersectando K en d puntos, es igual a$${\ displaystyle (q + 1) - {\ frac {q} {d}}}. Así, d divide q .
• En el caso especial de d = 2, los arcos máximos se conocen como hiperovalos que solo pueden existir si q es par.
• Un arco K que tiene un punto menos que un arco máximo siempre se puede extender de forma única a un arco máximo al agregar a K el punto en el que se encuentran todas las líneas que coinciden con K en d - 1 puntos. ^[2]
• En PG (2, q ) con q impar, no existen arcos máximos no triviales. ^[3]
• En PG (2,2 ^h ), existen arcos máximos para cada grado 2 ^t , 1 ≤ t ≤ h . ^[4]

Geometrías parciales [ editar ]

Uno puede construir geometrías parciales , derivadas de arcos máximos: ^[5]

• Sea K un arco máximo con grado d . Considerar la estructura de incidencia.$${\ displaystyle S (K) = (P, B, I)}, donde P contiene todos los puntos del plano proyectivo que no están en K , B contiene toda la línea del plano proyectivo que se interseca con K en d puntos, y la incidencia I es la inclusión natural. Esta es una geometría parcial:$${\ displaystyle pg (qd, q - {\ frac {q} {d}}, q - {\ frac {q} {d}} - d + 1)}.
• Considera el espacio $${\ displaystyle PG (3,2 ^ {h}) (h \ geq 1)}y dejar K un arco de grado máximo$${\ displaystyle d = 2 ^ {s} (1 \ leq s \ leq m)} en un subespacio bidimensional $${\ displaystyle \ pi}. Considere una estructura de incidencia$${\ displaystyle T_ {2} ^ {*} (K) = (P, B, I)}donde P contiene todos los puntos que no están en$${\ displaystyle \ pi}, B contiene todas las líneas que no están en$${\ displaystyle \ pi} y la intersección $${\ displaystyle \ pi}en un punto en K , y I es de nuevo la inclusión natural. $${\ displaystyle T_ {2} ^ {*} (K)} Es de nuevo una geometría parcial: $${\ displaystyle pg (2 ^ {h} -1, (2 ^ {h} +1) (2 ^ {m} -1), 2 ^ {m} -1) \,}.

 transformación de Möbius del plano complejo es una función racionalde la forma.

$${\ displaystyle f (z) = {\ frac {az + b} {cz + d}}}

de una variable compleja z ; aquí los coeficientes a , b , c , d son números complejos que satisfacen ad - bc ≠ 0.

Geométricamente, se puede obtener una transformación de Möbius realizando primero la proyección estereográfica desde el plano a la unidad de dos esferas , girando y moviendo la esfera a una nueva ubicación y orientación en el espacio, y luego realizando la proyección estereográfica (desde la nueva posición de la esfera ) al plano. ^[1] Estas transformaciones conservan los ángulos, mapean cada línea recta a una línea o círculo, y mapean cada círculo a una línea o círculo.

Las transformaciones de Möbius son las transformaciones proyectivas de la línea proyectiva compleja . Forman un grupo denominado grupo de Möbius , que es el grupo lineal proyectivo PGL (2, C ). Junto con sus subgrupos, tiene numerosas aplicaciones en matemáticas y física.

Las transformaciones de Möbius se nombran en honor a August Ferdinand Möbius ; también son diversamente nombrados homografías , transformaciones homográficas , transformaciones fraccionales lineales , transformaciones bilineales , o transformaciones lineales fraccionales .

Descripción general [ editar ]

Las transformaciones de Möbius se definen en el plano complejo extendido $${\ displaystyle {\ widehat {\ mathbf {C}}} = \ mathbf {C} \ cup \ {\ infty \}}(es decir, el plano complejo aumentado por el punto en el infinito ).

La proyección estereográfica identifica$${\ displaystyle {\ widehat {\ mathbf {C}}}}con una esfera, que entonces se llama la esfera de Riemann ; alternativamente,$${\ displaystyle {\ widehat {\ mathbf {C}}}}Se puede considerar como la compleja línea proyectiva. $${\ displaystyle \ mathbf {C} \ mathbf {P} ^ {1}}. Las transformaciones de Möbius son exactamente los mapas conformes biyectivos de la esfera de Riemann a sí misma, es decir, los automorfismos de la esfera de Riemann como una variedad compleja ; Alternativamente, son los automorfismos de$${\ displaystyle \ mathbf {C} \ mathbf {P} ^ {1}}Como una variedad algebraica. Por lo tanto, el conjunto de todas las transformaciones de Möbius forma un grupo bajo composición . Este grupo se llama el grupo de Möbius, y a veces se denota$${\ displaystyle \ operatorname {Aut} ({\ widehat {\ mathbf {C}}}) \,}.

El grupo de Möbius es isomorfo al grupo de isometrías que preservan la orientación del espacio 3 hiperbólico y, por lo tanto, juega un papel importante al estudiar las 3 variedades hiperbólicas .

En física , el componente de identidad del grupo de Lorentz actúa sobre la esfera celeste de la misma manera que el grupo de Möbius actúa sobre la esfera de Riemann. De hecho, estos dos grupos son isomorfos. Un observador que acelera a velocidades relativistas verá que el patrón de constelaciones que se ve cerca de la Tierra se transforma continuamente según las transformaciones infinitesimales de Möbius. Esta observación se toma a menudo como el punto de partida de la teoría del toristor .

Ciertos subgrupos del grupo de Möbius forman los grupos de automorfismo de las otras superficies de Riemann simplemente conectadas (el plano complejo y el plano hiperbólico ). Como tal, las transformaciones de Möbius desempeñan un papel importante en la teoría de las superficies de Riemann . El grupo fundamental de cada superficie de Riemann es un subgrupo discreto del grupo de Möbius (ver grupo de Fuchsian y grupo de Klein ). Un subgrupo discreto particularmente importante del grupo de Möbius es el grupo modular ; Es fundamental para la teoría de muchos fractales , formas modulares ,Curvas elípticas y ecuaciones pellianas .

Las transformaciones de Möbius pueden definirse de manera más general en espacios de dimensión n > 2 como los mapas de preservación de la orientación conformes biyectivos desde la n- esfera a la n- esfera. Tal transformación es la forma más general de mapeo conforme de un dominio. De acuerdo con el teorema de Liouville, una transformación de Möbius se puede expresar como una composición de traducciones, similitudes , transformaciones ortogonales e inversiones.

Definición [ editar ]

La forma general de una transformación de Möbius está dada por

$${\ displaystyle f (z) = {\ frac {az + b} {cz + d}}}

donde a , b , c , d son números complejos que satisfacen ad - bc ≠ 0 . Si ad = bc , la función racional definida anteriormente es una constante ya que

$${\ displaystyle f (z) = {\ frac {az + b} {cz + d}} = {\ frac {a (cz + d)} {c (cz + d)}} - {\ frac {ad- bc} {c (cz + d)}} = {\ frac {a} {c}}}

y por lo tanto no se considera una transformación de Möbius.

En el caso c ≠ 0 , esta definición se extiende a toda la esfera de Riemann definiendo

$${\ displaystyle f \ left ({\ frac {-d} {c}} \ right) = \ infty {\ text {y}} f (\ infty) = {\ frac {a} {c}}.}

Si c = 0 , definimos

$${\ displaystyle f (\ infty) = \ infty.}

Así, una transformación de Möbius es siempre una función holomórfica biyectiva de la esfera de Riemann a la esfera de Riemann.

El conjunto de todas las transformaciones de Möbius forma un grupo bajo composición . A este grupo se le puede dar la estructura de una variedad compleja de tal manera que la composición y la inversión sean mapas holomorfos . El grupo de Möbius es entonces un grupo complejo de mentiras . El grupo de Möbius se denota generalmente$${\ displaystyle \ operatorname {Aut} ({\ widehat {\ mathbf {C}}})}Como es el grupo de automorfismo de la esfera de Riemann.

Puntos fijos [ editar ]

Cada transformación de Möbius sin identidad tiene dos puntos fijos $${\ displaystyle \ gamma _ {1}, \ gamma _ {2}}en la esfera de riemann. Tenga en cuenta que los puntos fijos se cuentan aquí con multiplicidad ; Las transformaciones parabólicas son aquellas donde coinciden los puntos fijos. Cualquiera o ambos de estos puntos fijos pueden ser el punto en el infinito.

Determinando los puntos fijos [ editar ]

Los puntos fijos de la transformación.

$${\ displaystyle f (z) = {\ frac {az + b} {cz + d}}}

se obtienen resolviendo la ecuación de punto fijo f (γ) = γ. Para c ≠ 0, esto tiene dos raíces obtenidas al expandir esta ecuación a

$${\ displaystyle c \ gamma ^ {2} - (anuncio) \ gamma -b = 0 \,}

y aplicando la fórmula cuadrática . Las raices son

$${\ displaystyle \ gamma _ {1,2} = {\ frac {(anuncio) \ pm {\ sqrt {(anuncio) ^ {2} + 4bc}}} {2c}} = {\ frac {(anuncio) \ pm {\ sqrt {\ Delta}}} {2c}}}

con discriminante

$${\ displaystyle \ Delta = (\ operatorname {tr} {\ mathfrak {H}}) ^ {2} -4 \ operatorname {det} {\ mathfrak {H}} = (a + d) ^ {2} -4 (ad-bc)}.

Las transformaciones parabólicas tienen puntos fijos de coincidencia debido a cero discriminantes. Para c no nulo y no nulo discriminante, la transformada es elíptica o hiperbólica.

Cuando c = 0, la ecuación cuadrática degenera en una ecuación lineal y la transformación es lineal. Esto corresponde a la situación de que uno de los puntos fijos es el punto en el infinito. Cuando a ≠ d el segundo punto fijo es finito y viene dado por

$${\ displaystyle \ gamma = - {\ frac {b} {ad}}.

En este caso, la transformación será una transformación simple compuesta de traslaciones , rotaciones y dilataciones :

$${\ displaystyle z \ mapsto \ alpha z + \ beta. \,}

Si c = 0 y a = d , entonces ambos puntos fijos están en el infinito, y la transformación de Möbius corresponde a una traducción pura:

$${\ displaystyle z \ mapsto z + \ beta.}

Prueba topológica [ editar ]

Topológicamente, el hecho de que las transformaciones de Möbius (sin identidad) corrijan 2 puntos (con multiplicidad) corresponde a que la característica de Euler de la esfera es 2:

$${\ displaystyle \ chi ({\ hat {\ mathbf {C}}}) = 2.}

En primer lugar, el grupo lineal proyectivo PGL (2, K ) es marcadamente 3-transitivo  - para dos triples ordenados de puntos distintos, hay un mapa único que lleva un triple al otro, al igual que para las transformadas de Möbius, y por el mismo Prueba algebraica (esencialmente conteo de dimensiones , ya que el grupo es tridimensional). Así, cualquier mapa que arregle al menos 3 puntos es la identidad.

A continuación, se puede ver identificando el grupo de Möbius con $${\ displaystyle PGL (2, \ mathbb {C})}que cualquier función de Möbius es homotópica a la identidad. De hecho, cualquier miembro del grupo lineal general puede reducirse al mapa de identidad mediante la eliminación de Gauss-Jordan, lo que demuestra que el grupo lineal proyectivo también está conectado a la ruta, lo que proporciona una homotopía al mapa de identidad. El teorema de Lefschetz-Hopfestablece que que la suma de los índices (en este contexto, la multiplicidad) de los puntos fijos de un mapa con un número finito de puntos fijos es igual al número de Lefschetz del mapa, que en este caso es la traza del mapa de identidad en los grupos de homología, que es simplemente la característica de Euler.

Por el contrario, el grupo lineal proyectivo de la línea proyectiva real, PGL (2, R ) no necesita corregir ningún punto, por ejemplo$${\ displaystyle (1 + x) / (1-x)}no tiene puntos fijos (reales): como una transformación compleja corrige ± i ^{[nota 1]}  , mientras que el mapa 2x corrige los dos puntos de 0 y ∞. Esto corresponde al hecho de que la característica de Euler del círculo (línea proyectiva real) es 0, y por lo tanto el teorema de punto fijo de Lefschetz dice solo que debe corregir al menos 0 puntos, pero posiblemente más.

Forma normal [ editar ]

Las transformaciones de Möbius también se escriben a veces en términos de sus puntos fijos en la llamada forma normal . Primero tratamos el caso no parabólico, para el cual hay dos puntos fijos distintos.

Caso no parabólico :

Toda transformación no parabólica se conjuga con una dilatación / rotación, es decir, una transformación de la forma.

$${\ displaystyle z \ mapsto kz \,}

( k  ∈  C ) con puntos fijos en 0 y ∞. Para ver esto define un mapa.

$${\ displaystyle g (z) = {\ frac {z- \ gamma _ {1}} {z- \ gamma _ {2}}}}

que envía los puntos (γ ₁ , γ ₂ ) a (0, ∞). Aquí asumimos que γ ₁ y γ ₂ son distintos y finitos. Si uno de ellos ya está en el infinito, entonces g puede modificarse para corregir el infinito y enviar el otro punto a 0.

Si f tiene puntos fijos distintos (γ ₁ , γ ₂ ) entonces la transformación$${\ displaystyle gfg ^ {- 1}} tiene puntos fijos en 0 y ∞ y por lo tanto es una dilatación: $${\ displaystyle gfg ^ {- 1} (z) = kz}. La ecuación de punto fijo para la transformación f se puede escribir

$${\ displaystyle {\ frac {f (z) - \ gamma _ {1}} {f (z) - \ gamma _ {2}}} = k {\ frac {z- \ gamma _ {1}} {z - \ gamma _ {2}}}.}

Resolviendo para f da (en forma de matriz):

{\ displaystyle {\ mathfrak {H}} (k; \ gamma _ {1}, \ gamma _ {2}) = {\ begin {pmatrix} \ gamma _ {1} -k \ gamma _ {2} & ( k-1) \ gamma _ {1} \ gamma _ {2} \\ 1-k & k \ gamma _ {1} - \ gamma _ {2} \ end {pmatrix}}}

o, si uno de los puntos fijos está en el infinito:

{\ displaystyle {\ mathfrak {H}} (k; \ gamma, \ infty) = {\ begin {pmatrix} k & (1-k) \ gamma \\ 0 & 1 \ end {pmatrix}}.

A partir de las expresiones anteriores se pueden calcular las derivadas de f en los puntos fijos:

$${\ displaystyle f '(\ gamma _ {1}) = k \,} y $${\ displaystyle f '(\ gamma _ {2}) = 1 / k. \,}

Observe que, dado un ordenamiento de los puntos fijos, podemos distinguir uno de los multiplicadores ( k ) de fcomo la constante característica de f . Invertir el orden de los puntos fijos es equivalente a tomar el multiplicador inverso para la constante característica:

$${\ displaystyle {\ mathfrak {H}} (k; \ gamma _ {1}, \ gamma _ {2}) = {\ mathfrak {H}} (1 / k; \ gamma _ {2}, \ gamma _ {1}).}

Para transformaciones loxodrómicas, siempre que | k | > 1, uno dice que γ ₁ es el punto fijo repulsivo , y γ ₂ es el punto fijo atractivo . Para | k | <1 font="" invierten.="" los="" roles="" se="">

Caso parabólico :

En el caso parabólico solo hay un punto fijo γ. La transformación que envía ese punto a ∞ es

$${\ displaystyle g (z) = {\ frac {1} {z- \ gamma}}}

o la identidad si γ ya está en el infinito. La transformación$${\ displaystyle gfg ^ {- 1}} Corrige el infinito y es por lo tanto una traducción:

$${\ displaystyle gfg ^ {- 1} (z) = z + \ beta \ ,.}

Aquí, β se llama la longitud de la traducción . La fórmula de punto fijo para una transformación parabólica es entonces

$${\ displaystyle {\ frac {1} {f (z) - \ gamma}} = {\ frac {1} {z- \ gamma}} + \ beta.}

Resolviendo para f (en forma de matriz) da

{\ displaystyle {\ mathfrak {H}} (\ beta; \ gamma) = {\ begin {pmatrix} 1+ \ gamma \ beta & - \ beta \ gamma ^ {2} \\\ beta & 1- \ gamma \ beta \ end {pmatrix}}}

o, si γ = ∞:

{\ displaystyle {\ mathfrak {H}} (\ beta; \ infty) = {\ begin {pmatrix} 1 & \ beta \\ 0 & 1 \ end {pmatrix}}}

Tenga en cuenta que β no es la constante característica de f , que siempre es 1 para una transformación parabólica. A partir de las expresiones anteriores se puede calcular:

$${\ displaystyle f '(\ gamma) = 1. \,}

Polos de la transformación [ editar ]

El punto $${\ displaystyle z _ {\ infty} = - {\ frac {d} {c}}} se llama el polo de $${\ displaystyle {\ mathfrak {H}}}; es ese punto que se transforma al punto en el infinito bajo$${\ displaystyle {\ mathfrak {H}}}.

El polo inverso $${\ displaystyle Z _ {\ infty} = {\ frac {a} {c}}}Es ese punto al que se transforma el punto en el infinito. El punto a medio camino entre los dos polos es siempre el mismo que el punto a medio camino entre los dos puntos fijos:

$${\ displaystyle \ gamma _ {1} + \ gamma _ {2} = z _ {\ infty} + Z _ {\ infty}.}

Estos cuatro puntos son los vértices de un paralelogramo que a veces se denomina paralelogramo característico de la transformación.

Una transformada $${\ displaystyle {\ mathfrak {H}}}se puede especificar con dos puntos fijos γ ₁ , γ ₂ y el polo$${\ displaystyle z _ {\ infty}}.

{\ displaystyle {\ mathfrak {H}} = {\ begin {pmatrix} Z _ {\ infty} & - \ gamma _ {1} \ gamma _ {2} \\ 1 & -z _ {\ infty} \ end {pmatrix} }, \; \; Z _ {\ infty} = \ gamma _ {1} + \ gamma _ {2} -z _ {\ infty}.}

Esto nos permite derivar una fórmula para la conversión entre k y$${\ displaystyle z _ {\ infty}} dado $${\ displaystyle \ gamma _ {1}, \ gamma _ {2}}:

$${\ displaystyle z _ {\ infty} = {\ frac {k \ gamma _ {1} - \ gamma _ {2}} {1-k}}}

$${\ displaystyle k = {\ frac {\ gamma _ {2} -z _ {\ infty}} {\ gamma _ {1} -z _ {\ infty}}} = {\ frac {Z _ {\ infty} - \ gamma _ {1}} {Z _ {\ infty} - \ gamma _ {2}}} = {\ frac {ac \ gamma _ {1}} {ac \ gamma _ {2}}},}

que se reduce a

$${\ displaystyle k = {\ frac {(a + d) + {\ sqrt {(anuncio) ^ {2} + 4bc}}} {(a + d) - {\ sqrt {(anuncio) ^ {2} + 4bc}}}}.}

La última expresión coincide con una de las relaciones de valores propios (mutuamente recíprocas)$${\ displaystyle \ lambda _ {1} \ sobre \ lambda _ {2}} de la matriz

{\ displaystyle {\ mathfrak {H}} = {\ begin {pmatrix} a & b \\ c & d \ end {pmatrix}}}

representando la transformación (compare la discusión en la sección anterior sobre la constante característica de una transformación). Su polinomio característico es igual a

$${\ displaystyle \ det (\ lambda I_ {2} - {\ mathfrak {H}}) = \ lambda ^ {2} - \ operatorname {tr} {\ mathfrak {H}} \, \ lambda + \ det {\ mathfrak {H}} = \ lambda ^ {2} - (a + d) \ lambda + (ad-bc)}

que tiene raices

$${\ displaystyle \ lambda _ {i} = {\ frac {(a + d) \ pm {\ sqrt {(anuncio) ^ {2} + 4bc}}} {2}} = {\ frac {(a + d ) \ pm {\ sqrt {(a + d) ^ {2} -4 (ad-bc)}}} {2}} = c \ gamma _ {i} + d \.}

Transformaciones simples de Möbius y composición [ editar ]

Una transformación de Möbius se puede componer como una secuencia de transformaciones simples.

Las siguientes transformaciones simples también son transformaciones de Möbius:

$${\ displaystyle f (z) = z + b \ quad (a = 1, c = 0, d = 1)} es una traducción

$${\ displaystyle f (z) = az \ quad (b = 0, c = 0, d = 1)} es una combinación de un ( homothety y una rotación ) Si$${\ displaystyle | a | = 1} entonces es una rotación, si $${\ displaystyle a \ in \ mathbb {R}} entonces es un homothety

$${\ displaystyle f (z) = 1 / z \ quad (a = 0, b = 1, c = 1, d = 0)}( Inversión y reflexión respecto al eje real).

Composición de transformaciones simples [ editar ]

Dejar:

• $${\ displaystyle f_ {1} (z) = z + d / c \ quad}( traducción de d / c )
• $${\ displaystyle f_ {2} (z) = 1 / z \ quad}( Inversión y reflexión respecto al eje real).
• $${\ displaystyle f_ {3} (z) = {\ frac {bc-ad} {c ^ {2}}} z \ quad}( Homothety y rotación )
• $${\ displaystyle f_ {4} (z) = z + a / c \ quad}(traducción por a / c )

Entonces estas funciones pueden ser compuestas , dando

$${\ displaystyle f_ {4} \ circ f_ {3} \ circ f_ {2} \ circ f_ {1} (z) = f (z) = {\ frac {az + b} {cz + d}}}

Esta descomposición hace obvias muchas propiedades de la transformación de Möbius.

Propiedades elementales [ editar ]

Una transformación de Möbius es equivalente a una secuencia de transformaciones más simples. La composición hace obvias muchas propiedades de la transformación de Möbius.

Fórmula para la transformación inversa [ editar ]

La existencia de la transformación inversa de Möbius y su fórmula explícita se derivan fácilmente de la composición de las funciones inversas de las transformaciones más simples. Es decir, defina las funciones g ₁ , g ₂ , g ₃ , g _{4 de} modo que cada g _i sea ​​la inversa de f _i . Entonces la composicion

$${\ displaystyle g_ {1} \ circ g_ {2} \ circ g_ {3} \ circ g_ {4} (z) = f ^ {- 1} (z) = {\ frac {dz-b} {- cz + a}}} Da una fórmula para lo inverso.

Preservación de ángulos y círculos generalizados [ editar ]

A partir de esta descomposición, vemos que las transformaciones de Möbius traspasan todas las propiedades no triviales de la inversión del círculo . Por ejemplo, la conservación de los ángulos se reduce a probar que la inversión del círculo conserva los ángulos, ya que los otros tipos de transformaciones son la dilatación y las isometrías (traslación, reflexión, rotación), que conservan los ángulos de forma trivial.

Además, las transformaciones de Möbius mapean círculos generalizados a círculos generalizados ya que la inversión del círculo tiene esta propiedad. Un círculo generalizado es un círculo o una línea, esta última se considera como un círculo a través del punto en el infinito. Tenga en cuenta que una transformación de Möbius no necesariamente asigna círculos a círculos y de líneas a líneas: puede mezclar los dos. Incluso si asigna un círculo a otro círculo, no necesariamente asigna el centro del primer círculo al centro del segundo círculo.

Razón doble preservación [ editar ]

Las relaciones cruzadas son invariantes bajo las transformaciones de Möbius. Es decir, si una transformación de Möbius mapea cuatro puntos distintos$${\ displaystyle z_ {1}, z_ {2}, z_ {3}, z_ {4}} a cuatro puntos distintos $${\ displaystyle w_ {1}, w_ {2}, w_ {3}, w_ {4}} respectivamente, entonces

$${\ displaystyle {\ frac {(z_ {1} -z_ {3}) (z_ {2} -z_ {4})} {(z_ {2} -z_ {3}) (z_ {1} -z_ { 4})}} = {\ frac {(w_ {1} -w_ {3}) (w_ {2} -w_ {4})} {(w_ {2} -w_ {3}) (w_ {1} -w_ {4})}}.}

Si uno de los puntos $${\ displaystyle z_ {1}, z_ {2}, z_ {3}, z_ {4}}es el punto en el infinito, entonces la relación cruzada debe definirse tomando el límite apropiado; por ejemplo, la relación cruzada de$${\ displaystyle z_ {1}, z_ {2}, z_ {3}, \ infty} es

$${\ displaystyle {\ frac {(z_ {1} -z_ {3})} {(z_ {2} -z_ {3})}}.}

La relación cruzada de cuatro puntos diferentes es real si y solo si hay una línea o un círculo que pasa a través de ellos. Esta es otra forma de mostrar que las transformaciones de Möbius conservan los círculos generalizados.

Conjugación [ editar ]

Dos puntos z ₁ y z ₂ están conjugados con respecto a un círculo generalizado C , si, dado un círculo generalizado D que pasa a través de z ₁ y z ₂ y cortando C en dos puntos a y b , ( z ₁ , z ₂ ; a , b ) están en relación cruzada armónica (es decir, su relación cruzada es −1). Esta propiedad no depende de la elección del círculo D. A esta propiedad también se la conoce como simétrica con respecto a una línea o círculo. ^[2] [3]

Dos puntos z , z ^∗ se conjugan con respecto a una línea, si son simétricos con respecto a la línea. Dos puntos se conjugan con respecto a un círculo si son intercambiados por la inversión con respecto a este círculo.

El punto z ^∗ conjugado a z cuando L es la línea determinada por el vector e ^iθ en el punto z _{0 se} puede dar explícitamente como

$${\ displaystyle z ^ {*} = e ^ {2i \ theta} {\ overline {z-z_ {0}}} + z_ {0}.}

El punto z ^∗ conjugado a z cuando C es el círculo de radio r centrado en z _{0 se} puede dar explícitamente como

$${\ displaystyle z ^ {*} = {\ frac {r ^ {2}} {\ overline {z-z_ {0}}}} + z_ {0}}

Puesto que las transformaciones de Möbius conservan los círculos generalizados y las relaciones cruzadas, también preservan la conjugación.

Representaciones matriciales proyectivas [ editar ]

Con cada matriz invertible de 2 por 2.

{\ displaystyle {\ mathfrak {H}} = {\ begin {pmatrix} a & b \\ c & d \ end {pmatrix}}}

Podemos asociar la transformación de Möbius.

$${\ displaystyle f (z) = {\ frac {az + b} {cz + d}}.

La condición ad - bc ≠ 0 es equivalente a la condición de que el determinante de la matriz anterior sea distinto de cero, es decir, que la matriz sea invertible.

Es sencillo comprobar que el producto de dos matrices se asociará con la composición de las dos transformaciones de Möbius correspondientes. En otras palabras, el mapa.

$${\ displaystyle \ pi \ colon \ operatorname {GL} (2, \ mathbf {C}) \ to \ operatorname {Aut} ({\ widehat {\ mathbf {C}}})}

del grupo lineal general GL (2, C ) al grupo de Möbius, que envía la matriz$${\ displaystyle {\ mathfrak {H}}}A la transformación f , es un homomorfismo grupal .

Tenga en cuenta que cualquier matriz obtenida al multiplicar $${\ displaystyle {\ mathfrak {H}}}por un complejo escalar λ determina la misma transformación, por lo que una transformación de Möbius determina su matriz solo hasta múltiplos escalares. En otras palabras: el núcleo de π consta de todos los múltiplos escalares de la matriz de identidad I, y el primer teorema de isomorfismo de la teoría de grupos establece que el cociente grupo GL (2, C ) / (( C \ {0} ) Id) es Isomorfos para el grupo de Möbius. Este grupo cociente se conoce como grupo lineal proyectivo y generalmente se denomina PGL (2, C ).

$${\ displaystyle \ operatorname {Aut} ({\ widehat {\ mathbf {C}}}) \ cong \ operatorname {PGL} (2, \ mathbf {C}).}

La misma identificación de PGL (2, K ) con el grupo de transformaciones lineales fraccionarias y con el grupo de automorfismos proyectivos lineales de la línea proyectiva se mantiene sobre cualquier campo K , un hecho de interés algebraico, particularmente para campos finitos, aunque el caso de Los números complejos tienen el mayor interés geométrico.

La acción natural de PGL (2, C ) en la compleja línea proyectiva CP ¹ es exactamente la acción natural del grupo Möbius en la esfera de Riemann, donde la línea proyectiva CP ¹ y la esfera de Riemann se identifican de la siguiente manera:

$${\ displaystyle [z_ {1}: z_ {2}] \ leftrightarrow z_ {1} / z_ {2}.}

Aquí [ z ₁ : z ₂ ] son coordenadas homogéneas en CP ¹ ; el punto [1: 0] corresponde al punto ∞ de la esfera de Riemann. Al usar coordenadas homogéneas, se pueden simplificar muchos cálculos concretos que involucran transformaciones de Möbius, ya que no se requieren distinciones de caso relacionadas con.

Si se restringe $${\ displaystyle {\ mathfrak {H}}}a las matrices del determinante uno, el mapa π se restringe a un mapa suprayectivo del grupo lineal especial SL (2, C ) al grupo de Möbius; en la configuración restringida, el núcleo está formado por más y menos la identidad, y el grupo cociente SL (2, C ) / {± I }, indicado por PSL (2, C ), es por lo tanto también isomorfo al grupo de Möbius:

$${\ displaystyle \ operatorname {Aut} ({\ widehat {\ mathbf {C}}}) \ cong \ operatorname {PSL} (2, \ mathbf {C}).}

De esto podemos ver que el grupo de Möbius es un grupo de mentiras complejo de 3 dimensiones (o un grupo de mentiras real de 6 dimensiones). Es un grupo de mentiras semisimple no compacto .

Tenga en cuenta que hay dos matrices con determinantes de unidades que se pueden usar para representar cualquier transformación de Möbius dada. Es decir, SL (2, C ) es una portada doble de PSL (2, C ). Como SL (2, C ) está simplemente conectado , es la cobertura universal del grupo Möbius. Por lo tanto, el grupo fundamental del grupo de Möbius es Z ₂ .

Especificando una transformación por tres puntos [ editar ]

Dado un conjunto de tres puntos distintos z ₁ , z ₂ , z ₃ en la esfera de Riemann y un segundo conjunto de puntos distintos w ₁ , w ₂ , w ₃ , existe precisamente una transformación de Möbius f ( z ) con f ( z _i ) = w _i para i = 1,2,3. (En otras palabras: la acción del grupo de Möbius en la esfera de Riemann es marcadamente 3-transitiva ). Hay varias formas de determinar f ( z) De los conjuntos de puntos dados.

Mapeo primero a 0, 1, ∞ [ editar ]

Es fácil comprobar que la transformación de Möbius

$${\ displaystyle f_ {1} (z) = {\ frac {(z-z_ {1}) (z_ {2} -z_ {3})} {(z-z_ {3}) (z_ {2} - z_ {1})}}}

con matriz

{\ displaystyle {\ mathfrak {H}} _ {1} = {\ begin {pmatrix} z_ {2} -z_ {3} & - z_ {1} (z_ {2} -z_ {3}) \\ z_ {2} -z_ {1} & - z_ {3} (z_ {2} -z_ {1}) \ end {pmatrix}}}

mapas z ₁ , z ₂ , z ₃ a 0, 1, ∞, respectivamente. Si uno de los z _i es ∞, entonces la fórmula adecuada para$${\ displaystyle {\ mathfrak {H}} _ {1}}se obtiene del anterior al dividir primero todas las entradas por z _i y luego tomar el límite z _i → ∞.

Si $${\ displaystyle {\ mathfrak {H}} _ {2}}se define de manera similar para asignar w ₁ , w ₂ , w ₃ a 0, 1, ∞, luego la matriz$${\ displaystyle {\ mathfrak {H}}}el cual mapea z _1,2,3 a w _{1,2,3 se} convierte

$${\ displaystyle {\ mathfrak {H}} = {\ mathfrak {H}} _ {2} ^ {- 1} {\ mathfrak {H}} _ {1}.

El estabilizador de {0, 1, ∞} (como un conjunto desordenado) es un subgrupo conocido como el grupo anarmónico .

Fórmula determinante explícita [ editar ]

La ecuacion

$${\ displaystyle w = {\ frac {az + b} {cz + d}}}

Es equivalente a la ecuación de una hipérbola estándar.

$${\ displaystyle \, cwz-az + dw-b = 0}

en el plano ( z , w ). El problema de construir una transformación de Möbius.$${\ displaystyle {\ mathfrak {H}} (z)} mapeando un triple $${\ displaystyle (z_ {1}, z_ {2}, z_ {3})} a otro triple $${\ displaystyle (w_ {1}, w_ {2}, w_ {3})}es así equivalente a encontrar los coeficientes a , b , c , d de la hipérbola que pasa por los puntos$${\ displaystyle (z_ {i}, w_ {i})}. Se puede encontrar una ecuación explícita evaluando el determinante

{\ displaystyle \ det {\ begin {pmatrix} zw & z & w & 1 \\ z_ {1} w_ {1} & z_ {1} & w_ {1} & 1 \\ z_ {2} w_ {2} & z_ {2} & w_ {2} & 1 \\ z_ {3} w_ {3} & z_ {3} & w_ {3} & 1 \ end {pmatrix}} \,}

Por medio de una expansión de Laplace a lo largo de la primera fila. Esto da lugar a las fórmulas determinantes.

{\ displaystyle a = \ det {\ begin {pmatrix} z_ {1} w_ {1} & w_ {1} & 1 \\ z_ {2} w_ {2} & w_ {2} & 1 \\ z_ {3} w_ {3 } & w_ {3} & 1 \ end {pmatrix}} \,}

{\ displaystyle b = \ det {\ begin {pmatrix} z_ {1} w_ {1} & z_ {1} & w_ {1} \\ z_ {2} w_ {2} & z_ {2} & w_ {2} \\ z_ {3} w_ {3} & z_ {3} & w_ {3} \ end {pmatrix}} \,}

{\ displaystyle c = \ det {\ begin {pmatrix} z_ {1} & w_ {1} & 1 \\ z_ {2} & w_ {2} & 1 \\ z_ {3} & w_ {3} & 1 \ end {pmatrix}} \,}

{\ displaystyle d = \ det {\ begin {pmatrix} z_ {1} w_ {1} & z_ {1} & 1 \\ z_ {2} w_ {2} & z_ {2} & 1 \\ z_ {3} w_ {3 } & z_ {3} & 1 \ end {pmatrix}}}

para los coeficientes a, b, c, d de la matriz representativa{\ displaystyle \, {\ mathfrak {H}} = {\ begin {pmatrix} a & b \\ c & d \ end {pmatrix}}}. La matriz construida$${\ displaystyle {\ mathfrak {H}}} tiene determinante igual a $${\ displaystyle (z_ {1} -z_ {2}) (z_ {1} -z_ {3}) (z_ {2} -z_ {3}) (w_ {1} -w_ {2}) (w_ { 1} -w_ {3}) (w_ {2} -w_ {3})}que no se desvanece si la z _i resp. w _i son diferentes por pares, por lo que la transformación de Möbius está bien definida. Si uno de los puntos z _i o w _i es ∞, primero dividimos los cuatro determinantes por esta variable y luego tomamos el límite a medida que la variable se acerca a ∞.

Subgrupos del grupo Möbius [ editar ]

Si requerimos que los coeficientes a , b , c , d de una transformación de Möbius sean números reales con ad - bc = 1 , obtenemos un subgrupo del grupo de Möbius indicado como PSL (2, R ) . Este es el grupo de esas transformaciones de Möbius que mapean el semiplano superior H = x + i y  : y > 0 a sí mismo, y es igual al grupo de todos los mapas biholomorfos (o equivalentemente: biyectivo , conforme y preservación de la orientación) H→ H . Si se introduce una métrica adecuada , el semiplano superior se convierte en un modelo del plano hiperbólico H  ² , el modelo de semiplano de Poincaré , y PSL (2, R ) es el grupo de todas las isometrías de H  ^{2 que} conservan la orientación en este modelo.

El subgrupo de todas las transformaciones de Möbius que asignan el disco abierto D = z  : | z | <1 font=""> a sí mismo consiste en todas las transformaciones de la forma

$${\ displaystyle f (z) = e ^ {i \ phi} {\ frac {z + b} {{\ bar {b}} z + 1}}}

con $${\ displaystyle \ phi}∈ R , b ∈ C y | b | <1 .="" al="" biholomorphic="" biyectiva="" conserva="" de="" equivalentemente:="" es="" esto="" font="" grupo="" igual="" la="" mapas="" n="" nbsp="" ngulo-preservar="" o="" orientaci="" todos="" y="">D → D . Mediante la introducción de una métrica adecuada, el disco abierto se convierte en otro modelo de plano hiperbólico, el modelo de disco Poincaré , y este grupo es el grupo de todas las isometrías conserva la orientación de H  ² en este modelo.

Dado que los dos subgrupos anteriores sirven como grupos de isometría de H  ² , son isomorfos. Se da un isomorfismo concreto por conjugación con la transformación.

$${\ displaystyle f (z) = {\ frac {z + i} {iz + 1}}}

que mapea biyectivamente el disco de la unidad abierta a la mitad superior del plano.

Alternativamente, considere un disco abierto con radio r , centrado en ri . El modelo de disco de Poincaré en este disco se vuelve idéntico al modelo de mitad de plano superior cuando r se acerca a ∞.

Un máximo subgrupo compacto del grupo Möbius.$${\ displaystyle {\ mathcal {M}}}está dada por ^[4]

$${\ displaystyle {\ mathcal {M}} _ {0}: = \ left \ {z \ mapsto {\ frac {uz - {\ bar {v}}} {vz + {\ bar {u}}}}: | u | ^ {2} + | v | ^ {2} = 1 \ right \},}

y corresponde bajo el isomorfismo $${\ displaystyle {\ mathcal {M}} \ cong \ operatorname {PSL} (2, \ mathbf {C})}al grupo unitario especial proyectivo PSU (2, C ) que es isomorfo al grupo ortogonal especial SO (3) de rotaciones en tres dimensiones, y puede interpretarse como rotaciones de la esfera de Riemann. Cada subgrupo finito se conjuga en este grupo compacto máximo, y por lo tanto, estos se corresponden exactamente con los grupos poliédricos, los grupos de puntos en tres dimensiones .

Felix Klein usó grupos icosaédricos de las transformaciones de Möbius para dar una solución analítica a la ecuación quíntica en ( Klein 1888 ); una exposición moderna se da en. ^[5]

Si requerimos que los coeficientes a , b , c , d de una transformación de Möbius sean enteros con ad - bc = 1, obtenemos el grupo modular PSL (2, Z ), un subgrupo discreto de PSL (2, R ) importante en El estudio de las celosías en el plano complejo, funciones elípticas y curvas elípticas . Los subgrupos discretos de PSL (2, R ) se conocen como grupos fucsianos ; Son importantes en el estudio de las superficies de Riemann .

Clasificación [ editar ]

Se muestra una transformación hiperbólica. Las imágenes previas del círculo unitario son círculos de Apolonio con relación de distancia c / ay focos en - b / a y - d / c .

Para los mismos focos - b / a y - d / c,los círculos rojos se asignan a los rayos a través del origen.

En la siguiente discusión siempre asumiremos que la matriz representativa $${\ displaystyle {\ mathfrak {H}}} se normaliza tal que $${\ displaystyle \ det {\ mathfrak {H}} = ad-bc = 1}.

Las transformaciones de Möbius sin identidad se clasifican comúnmente en cuatro tipos: parabólica , elíptica , hiperbólica y loxodrómica , siendo las hiperbólicas una subclase de las loxodrómicas. La clasificación tiene tanto significación algebraica como geométrica. Geométricamente, los diferentes tipos dan como resultado diferentes transformaciones del plano complejo, como se ilustra en las siguientes figuras.

Los cuatro tipos pueden distinguirse mirando la huella $${\ displaystyle \ operatorname {tr} \, {\ mathfrak {H}} = a + d}. Tenga en cuenta que la traza es invariante en la conjugación , es decir,

$${\ displaystyle \ operatorname {tr} \, {\ mathfrak {GHG}} ^ {- 1} = \ operatorname {tr} \, {\ mathfrak {H}},}

y así, cada miembro de una clase de conjugación tendrá la misma huella. Cada transformación de Möbius se puede escribir de modo que su matriz representativa$${\ displaystyle {\ mathfrak {H}}}tiene un determinante (al multiplicar las entradas con un escalar adecuado). Dos transformaciones de Möbius$${\ displaystyle {\ mathfrak {H}}, {\ mathfrak {H}} '} (Ambos no son iguales a la transformada de identidad) con $${\ displaystyle \ det {\ mathfrak {H}} = \ det {\ mathfrak {H}} '= 1} se conjugan si y solo si $${\ displaystyle \ operatorname {tr} ^ {2} \, {\ mathfrak {H}} = \ operatorname {tr} ^ {2} \, {\ mathfrak {H}} '.}

Transforma parabólicos [ editar ]

El cuadro de Smith , utilizado por los ingenieros eléctricos para analizar las líneas de transmisión , es una representación visual de la transformación parabólica de Möbius z = (Γ + 1) / (- Γ + 1). Cada punto en el gráfico Smith representa simultáneamente un valor de z (abajo a la izquierda) y el valor correspondiente de Γ (abajo a la derecha), para | Γ | <1 .="" font="">

Una transformación de Möbius sin identidad definida por una matriz. $${\ displaystyle {\ mathfrak {H}}}de determinante se dice que es parabólico si

$${\ displaystyle \ operatorname {tr} ^ {2} {\ mathfrak {H}} = (a + d) ^ {2} = 4}

(por lo que la traza es más o menos 2; cualquiera puede ocurrir para una transformación dada, ya que $${\ displaystyle {\ mathfrak {H}}}Se determina solo hasta la firma). De hecho una de las opciones para$${\ displaystyle {\ mathfrak {H}}}tiene el mismo polinomio característico X ² −2 X +1 que la matriz de identidad y, por lo tanto, es unipotente . Una transformada de Möbius es parabólica si y solo si tiene exactamente un punto fijo en el plano complejo extendido $${\ displaystyle {\ widehat {\ mathbf {C}}} = \ mathbf {C} \ cup \ {\ infty \}}, lo que sucede si y solo si puede ser definido por una matriz conjugada para

{\ displaystyle {\ begin {pmatrix} 1 & 1 \\ 0 & 1 \ end {pmatrix}}}

que describe una traducción en el plano complejo.

El conjunto de todas las transformaciones de Möbius parabólicos con un dado punto fijo en$${\ displaystyle {\ widehat {\ mathbf {C}}}}, junto con la identidad, forma un subgrupo isomorfo al grupo de matrices.

{\ displaystyle \ left \ {{\ begin {pmatrix} 1 & b \\ 0 & 1 \ end {pmatrix}} \ mid b \ in \ mathbf {C} \ right \};}

Este es un ejemplo del radical unipotente de un subgrupo de Borel (del grupo de Möbius o de SL (2, C ) para el grupo de la matriz; la noción se define para cualquier grupo de Lie reductivo ).

Constante característica [ editar ]

Todas las transformaciones no parabólicas tienen dos puntos fijos y están definidas por un conjugado de matriz para

{\ displaystyle {\ begin {pmatrix} \ lambda & 0 \\ 0 & \ lambda ^ {- 1} \ end {pmatrix}}}

con el número complejo λ no es igual a 0, 1 o −1, correspondiente a una dilatación / rotación a través de la multiplicación por el número complejo k = λ ² , llamado la constante característica o el multiplicador de la transformación.

Transformaciones elípticas [ editar ]

Se dice que la transformación es elíptica si puede representarse por una matriz$${\ displaystyle {\ mathfrak {H}}}cuyo rastro es real con

{\ displaystyle 0 \ leq \ operatorname {tr} ^ {2} {\ mathfrak {H}} <4 .="" font="">

Una transformada es elíptica si y solo si | λ | = 1 y λ ≠ ± 1. Escritura$${\ displaystyle \ lambda = e ^ {i \ alpha}}, una transformada elíptica es conjugada a

{\ displaystyle {\ begin {pmatrix} \ cos \ alpha & - \ sin \ alpha \\\ sin \ alpha & \ cos \ alpha \ end {pmatrix}}}

con α real.

Tenga en cuenta que para cualquier $${\ displaystyle {\ mathfrak {H}}}con la constante característica k , la constante característica de$${\ displaystyle {\ mathfrak {H}} ^ {n}}es k ⁿ . Por lo tanto, todas las transformaciones de Möbius de orden finito son transformaciones elípticas, es decir, exactamente aquellas donde λ es una raíz de la unidad , o, equivalentemente, donde α es un múltiplo racional de π . La posibilidad más simple de un múltiplo fraccionario es α = π / 2, que también es el caso único de$${\ displaystyle \ operatorname {tr} {\ mathfrak {H}} = 0}, también se denota como una transformada circular ; esto corresponde geométricamente a la rotación en 180 ° alrededor de dos puntos fijos. Esta clase se representa en forma de matriz como:

{\ displaystyle {\ begin {pmatrix} 0 & -1 \\ 1 & 0 \ end {pmatrix}}.}

Hay 3 representantes fijando {0, 1, ∞}, que son las tres transposiciones en el grupo de simetría de estos 3 puntos: $${\ displaystyle 1 / z,}que corrige 1 e intercambia 0 con ∞ (rotación de 180 ° sobre los puntos 1 y −1),$${\ displaystyle 1-z}, que corrige ∞e intercambia 0 con 1 (rotación de 180 ° sobre los puntos 1/2 y ∞ ), y$${\ displaystyle z / (z-1)}que corrige 0 e intercambia 1 con ∞ (rotación de 180 ° sobre los puntos 0 y 2).

Transformaciones hiperbólicas [ editar ]

Se dice que la transformada es hiperbólica si puede representarse por una matriz$${\ displaystyle {\ mathfrak {H}}}cuyo rastro es real con

{\ displaystyle \ operatorname {tr} ^ {2} {\ mathfrak {H}}> 4. \,}

Una transformada es hiperbólica si y solo si λ es real y positiva.

Transformaciones loxodrómicas [ editar ]

Se dice que la transformada es loxodrómica si$${\ displaystyle \ operatorname {tr} ^ {2} {\ mathfrak {H}}}no está en [0,4]. Una transformación es loxodrómica si y solo si$${\ displaystyle | \ lambda | \ neq 1}.

Históricamente, la navegación por loxódromo o línea de rumbo se refiere a una trayectoria de rumbo constante ; el camino resultante es una espiral logarítmica , similar en forma a las transformaciones del plano complejo que hace una transformación loxodrómica de Möbius. Vea las figuras geométricas a continuación.

Clasificación general [ editar ]

Transformación	Traza al cuadrado	Multiplicadores	Representante de clase
Circular	σ = 0	k = −1	{\ displaystyle {\ begin {pmatrix} i & 0 \\ 0 & -i \ end {pmatrix}}}	z ↦ - z
Elíptico	0 ≤ σ <4 font="">	| k | = 1 $${\ displaystyle k = e ^ {\ pm i \ theta} \ neq 1}	{\ displaystyle {\ begin {pmatrix} e ^ {i \ theta / 2} & 0 \\ 0 & e ^ {- i \ theta / 2} \ end {pmatrix}}}	z ↦ e i θ z
Parabólico	σ = 4	k = 1	{\ displaystyle {\ begin {pmatrix} 1 & a \\ 0 & 1 \ end {pmatrix}}}	z ↦ z + a
Hiperbólico	4 <σ <∞	$${\ displaystyle k \ in \ mathbf {R} ^ {+}} $${\ displaystyle k = e ^ {\ pm \ theta} \ neq 1}	{\ displaystyle {\ begin {pmatrix} e ^ {\ theta / 2} & 0 \\ 0 & e ^ {- \ theta / 2} \ end {pmatrix}}}	z ↦ e θ z
Loxodromic	σ ∈ C \ [0,4]	$${\ displaystyle | k | \ neq 1} $${\ displaystyle k = \ lambda ^ {2}, \ lambda ^ {- 2}}	{\ displaystyle {\ begin {pmatrix} \ lambda & 0 \\ 0 & \ lambda ^ {- 1} \ end {pmatrix}}}	z ↦ kz

El caso real y una nota sobre terminología [ editar ]

Sobre los números reales (si los coeficientes deben ser reales), no hay transformaciones loxodrómicas no hiperbólicas, y la clasificación es en elíptica, parabólica e hiperbólica, como para las cónicas reales . La terminología se debe a que considera la mitad del valor absoluto de la traza, | tr | / 2, ya que la excentricidad de la transformación - la división por 2 corrige la dimensión, por lo que la identidad tiene excentricidad 1 (tr / n se usa a veces como una alternativa para la traza por esta razón), y el valor absoluto corrige la traza que solo se define hasta un factor de ± 1 debido al trabajo en PSL. Alternativamente se puede usar la mitad de la traza al cuadrado.como proxy de la excentricidad al cuadrado, como se hizo anteriormente; estas clasificaciones (pero no los valores exactos de excentricidad, ya que los valores de cuadratura y los valores absolutos son diferentes) concuerdan con trazas reales pero no con trazas complejas. La misma terminología se usa para la clasificación de los elementos de SL (2, R ) (la doble cobertura), y las clasificaciones análogas se usan en otros lugares. Las transformaciones de Loxodromic son un fenómeno esencialmente complejo, y corresponden a las excentricidades complejas.

Interpretación geométrica de la constante característica [ editar ]

La siguiente imagen muestra (después de la transformación estereográfica de la esfera al plano) los dos puntos fijos de una transformación de Möbius en el caso no parabólico:

La constante característica se puede expresar en términos de su logaritmo :

$${\ displaystyle e ^ {\ rho + \ alpha i} = k. \;}

Cuando se expresa de esta manera, el número real ρ se convierte en un factor de expansión. Indica cuán repulsivo es el punto fijo γ ₁ y cuán atractivo es γ ₂ . El número real α es un factor de rotación, que indica en qué medida la transformada gira el plano en sentido antihorario alrededor de γ ₁ y en sentido horario alrededor de γ ₂.

Transformaciones elípticas [ editar ]

Si ρ = ​​0, entonces los puntos fijos no son atractivos ni repulsivos sino indiferentes, y se dice que la transformación es elíptica . Estas transformaciones tienden a mover todos los puntos en círculos alrededor de los dos puntos fijos. Si uno de los puntos fijos está en el infinito, esto es equivalente a hacer una rotación afín alrededor de un punto.

Si tomamos el subgrupo de un solo parámetro generado por cualquier transformación elíptica de Möbius, obtenemos una transformación continua, de modo que cada transformación en el subgrupo corrija los mismosdos puntos. Todos los demás puntos fluyen a lo largo de una familia de círculos que se anidan entre los dos puntos fijos en la esfera de Riemann. En general, los dos puntos fijos pueden ser dos puntos distintos.

Esto tiene una importante interpretación física. Imagina que algún observador gira con una velocidad angular constante alrededor de algún eje. Luego podemos tomar los dos puntos fijos como los polos norte y sur de la esfera celeste. La apariencia del cielo nocturno ahora se transforma de manera continua exactamente de la manera descrita por el subgrupo de un parámetro de transformaciones elípticas que comparten los puntos fijos 0, ∞, y el número α corresponde a la velocidad angular constante de nuestro observador.

Aquí hay algunas figuras que ilustran el efecto de una transformación elíptica de Möbius en la esfera de Riemann (después de la proyección estereográfica al plano):

Estas imágenes ilustran el efecto de una sola transformación de Möbius. El subgrupo de un parámetro que genera continuamente mueve puntos a lo largo de la familia de arcos circulares sugeridos por las imágenes.

Transformaciones hiperbólicas [ editar ]

Si α es cero (o un múltiplo de 2 π ), entonces se dice que la transformación es hiperbólica . Estas transformaciones tienden a mover puntos a lo largo de caminos circulares desde un punto fijo hacia el otro.

Si tomamos el subgrupo de un solo parámetro generado por cualquier transformación hiperbólica de Möbius, obtenemos una transformación continua, de manera que cada transformación en el subgrupo corrige los mismosdos puntos. Todos los demás puntos fluyen a lo largo de una cierta familia de arcos circulares que se alejan del primer punto fijo y hacia el segundo punto fijo. En general, los dos puntos fijos pueden ser dos puntos distintos en la esfera de Riemann.

Esto también tiene una importante interpretación física. Imagina que un observador acelera (con una magnitud constante de aceleración) en la dirección del polo norte en su esfera celeste. Luego, la apariencia del cielo nocturno se transforma exactamente de la manera descrita por el subgrupo de un parámetro de transformaciones hiperbólicas que comparten los puntos fijos 0, ∞, con el número real ρ correspondiente a la magnitud de su vector de aceleración. Las estrellas parecen moverse a lo largo de las longitudes, alejándose del polo sur hacia el polo norte. (Las longitudes aparecen como arcos circulares bajo proyección estereográfica desde la esfera hasta el plano.)

Aquí hay algunas figuras que ilustran el efecto de una transformación hiperbólica de Möbius en la esfera de Riemann (después de la proyección estereográfica al plano):

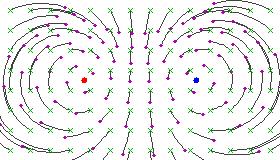
Estas imágenes se parecen a las líneas de campo de una carga eléctrica positiva y negativa ubicada en los puntos fijos, porque las líneas de flujo circular subtienden un ángulo constante entre los dos puntos fijos.

Transformaciones loxodrómicas [ editar ]

Si tanto ρ como α son distintos de cero, entonces se dice que la transformación es loxodrómica . Estas transformaciones tienden a mover todos los puntos en caminos en forma de S de un punto fijo al otro.

La palabra " loxódromo " proviene del griego: "λοξος (loxos), inclinación + δρόμος (dromos), curso ". Cuando navega en un rumbo constante , si mantiene un rumbo de (digamos) noreste, finalmente terminará navegando alrededor del polo norte en una espiral logarítmica . En la proyección de mercator, tal curso es una línea recta, ya que los polos norte y sur se proyectan hasta el infinito. El ángulo que subtiende el loxódromo en relación con las líneas de longitud (es decir, su pendiente, la "tensión" de la espiral) es el argumento de k. Por supuesto, las transformaciones de Möbius pueden tener sus dos puntos fijos en cualquier lugar, no solo en los polos norte y sur. Pero cualquier transformación loxodrómica se conjugará con una transformación que mueva todos los puntos a lo largo de tales loxódromos.

Si tomamos el subgrupo de un solo parámetro generado por cualquier transformación loxodrómica de Möbius, obtenemos una transformación continua, de modo que cada transformación en el subgrupo corrija los mismosdos puntos. Todos los demás puntos fluyen a lo largo de una determinada familia de curvas, alejándose del primer punto fijo y hacia el segundo punto fijo. A diferencia del caso hiperbólico, estas curvas no son arcos circulares, pero ciertas curvas que, bajo la proyección estereográfica desde la esfera al plano, aparecen como curvas espirales que giran en sentido contrario a las agujas del reloj infinitamente alrededor de un punto fijo y giran en el sentido de las agujas del reloj infinitamente a menudo alrededor del otro punto fijo. En general, los dos puntos fijos pueden ser dos puntos distintos en la esfera de Riemann.

Probablemente pueda adivinar la interpretación física en el caso cuando los dos puntos fijos son 0,: un observador que está girando (con velocidad angular constante) alrededor de algún eje y se mueve a lo largo del mismo eje, verá la apariencia del cielo nocturno transformar de acuerdo con el subgrupo de un parámetro de transformaciones loxodrómicas con puntos fijos 0,, y con ρ, α determinado respectivamente por la magnitud de las velocidades lineales y angulares reales.

La proyección estereográfica [ editar ]

Estas imágenes muestran las transformaciones de Möbius proyectadas estereográficamente sobre la esfera de Riemann . Tenga en cuenta, en particular, que cuando se proyecta en una esfera, el caso especial de un punto fijo en el infinito no es diferente de tener los puntos fijos en una ubicación arbitraria.

Un punto fijo en el infinito.
Elíptico	Hiperbólico	Loxodromic
Puntos fijos diametralmente opuestos.
Elíptico	Hiperbólico	Loxodromic
Puntos fijos en un lugar arbitrario.
Elíptico	Hiperbólico	Loxodromic

Iterando una transformación [ editar ]

Si una transformacion $${\ displaystyle {\ mathfrak {H}}}tiene puntos fijos γ ₁ , γ ₂ y una constante característica k , luego$${\ displaystyle {\ mathfrak {H}} '= {\ mathfrak {H}} ^ {n}} tendrá $${\ displaystyle \ gamma _ {1} '= \ gamma _ {1}, \ gamma _ {2}' = \ gamma _ {2}, k '= k ^ {n}}.

Esto se puede usar para iterar una transformación, o para animarla, dividiéndola en pasos.

Estas imágenes muestran tres puntos (rojo, azul y negro) iterados continuamente bajo transformaciones con varias constantes características.

Y estas imágenes demuestran lo que sucede cuando transformas un círculo bajo transformadas Hiperbólicas, Elípticas y Loxodrómicas. Tenga en cuenta que en las imágenes elípticas y loxodrómicas, el valor α es 1/10.

  

Polos de la transformación [ editar ]

El punto

$${\ displaystyle z _ {\ infty} = - {\ frac {d} {c}}}

se llama el polo de $${\ displaystyle {\ mathfrak {H}}}; es ese punto que se transforma al punto en el infinito bajo$${\ displaystyle {\ mathfrak {H}}}.

El polo inverso

$${\ displaystyle Z _ {\ infty} = {\ frac {a} {c}}}

Es ese punto al que se transforma el punto en el infinito. El punto a medio camino entre los dos polos es siempre el mismo que el punto a medio camino entre los dos puntos fijos:

$${\ displaystyle \ gamma _ {1} + \ gamma _ {2} = z _ {\ infty} + Z _ {\ infty}.}

Estos cuatro puntos son los vértices de un paralelogramo que a veces se denomina paralelogramo característico de la transformación.

Una transformada $${\ displaystyle {\ mathfrak {H}}}se puede especificar con dos puntos fijos γ ₁ , γ ₂ y el polo$${\ displaystyle z _ {\ infty}}.

{\ displaystyle {\ mathfrak {H}} = {\ begin {pmatrix} Z _ {\ infty} & - \ gamma _ {1} \ gamma _ {2} \\ 1 & -z _ {\ infty} \ end {pmatrix} }, \; \; Z _ {\ infty} = \ gamma _ {1} + \ gamma _ {2} -z _ {\ infty}.}

Esto nos permite derivar una fórmula para la conversión entre k y$${\ displaystyle z _ {\ infty}} dado $${\ displaystyle \ gamma _ {1}, \ gamma _ {2}}:

$${\ displaystyle z _ {\ infty} = {\ frac {k \ gamma _ {1} - \ gamma _ {2}} {1-k}}}

$${\ displaystyle k = {\ frac {\ gamma _ {2} -z _ {\ infty}} {\ gamma _ {1} -z _ {\ infty}}} = {\ frac {Z _ {\ infty} - \ gamma _ {1}} {Z _ {\ infty} - \ gamma _ {2}}} = {\ frac {ac \ gamma _ {1}} {ac \ gamma _ {2}}},}

que se reduce a

$${\ displaystyle k = {\ frac {(a + d) + {\ sqrt {(anuncio) ^ {2} + 4bc}}} {(a + d) - {\ sqrt {(anuncio) ^ {2} + 4bc}}}}.}

La última expresión coincide con una de las relaciones de valores propios (mutuamente recíprocas)$${\ displaystyle \ lambda _ {1} \ sobre \ lambda _ {2}} de la matriz

{\ displaystyle {\ mathfrak {H}} = {\ begin {pmatrix} a & b \\ c & d \ end {pmatrix}}}

representando la transformación (compare la discusión en la sección anterior sobre la constante característica de una transformación). Su polinomio característico es igual a

$${\ displaystyle \ det (\ lambda I_ {2} - {\ mathfrak {H}}) = \ lambda ^ {2} - \ operatorname {tr} {\ mathfrak {H}} \, \ lambda + \ det {\ mathfrak {H}} = \ lambda ^ {2} - (a + d) \ lambda + (ad-bc)}

que tiene raices

$${\ displaystyle \ lambda _ {i} = {\ frac {(a + d) \ pm {\ sqrt {(anuncio) ^ {2} + 4bc}}} {2}} = {\ frac {(a + d ) \ pm {\ sqrt {(a + d) ^ {2} -4 (ad-bc)}}} {2}} = c \ gamma _ {i} + d \.}

Dimensiones superiores [ editar ]

En dimensiones más altas, una transformación de Möbius es un homeomorfismo de$${\ displaystyle {\ overline {\ mathbb {R} ^ {n}}}}, la compactación de un punto de$${\ displaystyle \ mathbb {R} ^ {n}}, que es una composición finita de inversiones en esferas y reflexiones en hiperplanos . ^[6] El teorema de Liouville en geometría conforme establece que en la dimensión al menos tres, todas las transformaciones conformes son transformaciones de Möbius. Cada transformación de Möbius se puede poner en la forma

$${\ displaystyle f (x) = b + {\ frac {\ alpha A (xa)} {| xa | ^ {\ epsilon}}}}

dónde $${\ displaystyle a, b \ in \ mathbb {R} ^ {n}}, $${\ displaystyle \ alpha \ in \ mathbb {R}}, $${\ displaystyle A}es una matriz ortogonal , y$${\ displaystyle \ epsilon}es 0 o 2. El grupo de transformaciones de Möbius también se llama el grupo de Möbius . ^[7]

Las transformaciones de Möbius que preservan la orientación forman el componente conectado de la identidad en el grupo de Möbius. En dimensión n = 2 , las transformaciones de Möbius que preservan la orientación son exactamente los mapas de la esfera de Riemann que se cubren aquí. Los de orientación inversa se obtienen de estos por conjugación compleja. ^[8]

El dominio de las transformaciones de Möbius, es decir, $${\ displaystyle {\ overline {\ mathbb {R} ^ {n}}}}, es homeomorfo a la esfera n- dimensional.$${\ displaystyle S ^ {n}}. El isomorfismo canónico entre estos dos espacios es la transformada de Cayley , que en sí misma es una transformación de Möbius de$${\ displaystyle {\ overline {\ mathbb {R} ^ {n + 1}}}}. Esta identificación significa que las transformaciones de Möbius también se pueden considerar como isomorfismos conformes de$${\ displaystyle S ^ {n}}. La n- esfera, junto con la acción del grupo de Möbius, es una estructura geométrica (en el sentido del programa Erlangen de Klein ) llamada geometría de Möbius . ^[9]

Aplicaciones [ editar ]

Transformación de Lorentz [ editar ]

Artículo principal: Transformación de Lorentz.

Varios autores notaron un isomorfismo del grupo de Möbius con el grupo de Lorentz : Sobre la base del trabajo anterior de Felix Klein (1893, 1897) ^[10] sobre funciones automáticas relacionadas con la geometría hiperbólica y la geometría de Möbius, Gustav Herglotz (1909) ^[11] mostró que los movimientos hiperbólicos (es decir, los automorfismos isométricos de un espacio hiperbólico ) que transforman la esfera unitaria en sí mismos corresponden a las transformaciones de Lorentz, mediante las cuales Herglotz pudo clasificar las transformaciones de Lorentz de un parámetro en grupos loxodrómicos, elípticos, hiperbólicos y parabólicos. Otros autores incluyenEmil Artin (1957), ^[12] HSM Coxeter (1965), ^[13] y Roger Penrose y Wolfgang Rindler(1984). ^[14]

El espacio de Minkowski consiste en el espacio de coordenadas reales de cuatro dimensiones R ^{4 que} consiste en el espacio de cuádruples ordenados ( x ₀ , x ₁ , x ₂ , x ₃ ) de números reales, junto con una forma cuadrática

$${\ displaystyle Q (x_ {0}, x_ {1}, x_ {2}, x_ {3}) = x_ {0} ^ {2} -x_ {1} ^ {2} -x_ {2} ^ { 2} -x_ {3} ^ {2}.}

Tomando la terminología de la relatividad especial , los puntos con Q  > 0 se consideran cronológicos ; Además, si x ₀  > 0, el punto se llama apuntando al futuro . Los puntos con Q  <0 font="" llaman="" nbsp="" se="">espaciales . El cono nulo Sconsiste en aquellos puntos donde Q  = 0; el futuro cono nulo N ⁺ son aquellos puntos en el cono nulo con x ₀  > 0. La esfera celeste se identifica con la colección de rayos en N ⁺ cuyo punto inicial es el origen deR ⁴ . La colección de transformaciones lineales en R ⁴ con determinante positivo conserva la forma cuadrática Q y conserva la dirección del tiempo desde el grupo de Lorentz restringido SO ⁺ (1,3).

En relación con la geometría de la esfera celeste, el grupo de transformaciones SO ⁺ (1,3) se identifica con el grupo PSL (2, C ) de las transformaciones de Möbius de la esfera. A cada ( x ₀ , x ₁ , x ₂ , x ₃ ) ∈  R ⁴ , asocie la matriz hermitiana

{\ displaystyle X = {\ begin {bmatrix} x_ {0} + x_ {1} & x_ {2} + ix_ {3} \\ x_ {2} -ix_ {3} & x_ {0} -x_ {1} \ fin {bmatrix}}.

El determinante de la matriz X es igual a Q ( x ₀ , x ₁ , x ₂ , x ₃ ). El grupo lineal especial actúa sobre el espacio de tales matrices a través de

$${\ displaystyle X \ mapsto AXA ^ {*}}

( 1 )

para cada A ∈ SL (2, C ), y esta acción de SL (2, C ) conserva el determinante de X porque det A = 1 . Dado que el determinante de X se identifica con la forma cuadrática Q , SL (2, C ) actúa mediante transformaciones de Lorentz. Por motivos dimensionales, SL (2, C ) cubre un vecindario de la identidad de SO (1,3). Dado que SL (2, C ) está conectado, cubre todo el grupo de Lorentz SO ⁺ restringido (1,3). Además, dado que el núcleo de la acción ( 1 ) es el subgrupo {± I}, luego pasar al grupo de cocientes le da isomorfismo al grupo

$${\ displaystyle \ operatorname {PSL} (2, \ mathbf {C}) \ cong SO ^ {+} (1,3).}

( 2 )

Enfocando ahora la atención en el caso cuando ( x ₀ , x ₁ , x ₂ , x ₃ ) es nulo, la matriz X tiene determinante cero y, por lo tanto, se divide como el producto externo de un complejo de dos vectores ξ con su conjugado complejo:

$${\ displaystyle X = \ xi {\ bar {\ xi}} ^ {T} = \ xi \ xi ^ {*}.}

( 3 )

SL (2, C ) actúa sobre el vector de dos componentes ξ de una manera compatible con ( 1 ). Ahora está claro que el núcleo de la representación de SL (2, C ) en matrices hermitianas es {± I }.

La acción de la PSL (2, C ) en la esfera celeste también se puede describir geométricamente utilizando una proyección estereográfica . Considere primero el hiperplano en R ⁴ dado por x ₀  = 1. La esfera celeste puede identificarse con la esfera S ⁺ de intersección del hiperplano con el cono nulo futuro N ⁺ . La proyección estereográfica desde el polo norte (1,0,0,1) de esta esfera sobre el plano x ₃  = 0 toma un punto con coordenadas (1, x ₁ , x ₂ , x ₃ ) con

$${\ displaystyle x_ {1} ^ {2} + x_ {2} ^ {2} + x_ {3} ^ {2} = 1}

al punto

$${\ displaystyle \ left (1, {\ frac {x_ {1}} {1-x_ {3}}}, {\ frac {x_ {2}} {1-x_ {3}}}, 0 \ right) .}

Introduciendo la coordenada compleja

$${\ displaystyle \ zeta = {\ frac {x_ {1} + ix_ {2}} {1-x_ {3}}},}

la proyección estereográfica inversa da la siguiente fórmula para un punto ( x ₁ , x ₂ , x ₃ ) en S ⁺ :

{\ displaystyle {\ begin {alineado} x_ {1} & = {\ frac {\ zeta + {\ bar {\ zeta}}} {\ zeta {\ bar {\ zeta}} + 1}} \\ x_ { 2} & = {\ frac {\ zeta - {\ bar {\ zeta}}} {i (\ zeta {\ bar {\ zeta}} + 1)}} \\ x_ {3} & = {\ frac { \ zeta {\ bar {\ zeta}} - 1} {\ zeta {\ bar {\ zeta}} + 1}}. \ end {alineado}}}

( 4 )

La acción de SO ⁺ (1,3) en los puntos de N ⁺ no conserva el hiperplano S ⁺ , sino que actúa sobre los puntos de S ⁺ y luego se vuelve a escalar para que el resultado nuevamente en S ⁺ dé una acción de SO ⁺ ( 1,3) en la esfera que pasa a una acción sobre la variable compleja ζ. De hecho, esta acción es por transformaciones lineales fraccionarias, aunque esto no se ve fácilmente en esta representación de la esfera celeste. A la inversa, para cualquier transformación lineal fraccional de la variable goes se pasa a una transformación de Lorentz única en N ⁺ , posiblemente después de un reescalado adecuado (determinado de forma única).

Una descripción más invariable de la proyección estereográfica que permite ver la acción más claramente es considerar la variable ζ =  z : w como una relación de un par de coordenadas homogéneas para la línea proyectiva compleja CP ¹ . La proyección estereográfica pasa a una transformación de C ²  - {0} a N ⁺ que es homogénea de grado dos con respecto a escalas reales

$${\ displaystyle (z, w) \ mapsto (x_ {0}, x_ {1}, x_ {2}, x_ {3}) = (z {\ bar {z}} + w {\ bar {w}} , z {\ bar {z}} - w {\ bar {w}}, z {\ bar {w}} + w {\ bar {z}}, i ^ {- 1} (z {\ bar {w }} - w {\ bar {z}}))}

( 5 )

que está de acuerdo con ( 4 ) en la restricción a escalas en las que$${\ displaystyle z {\ bar {z}} + w {\ bar {w}} = 1.}Los componentes de ( 5 ) son precisamente los obtenidos del producto exterior.

{\ displaystyle {\ begin {bmatrix} x_ {0} + x_ {1} & x_ {2} + ix_ {3} \\ x_ {2} -ix_ {3} & x_ {0} -x_ {1} \ end { bmatrix}} = 2 {\ begin {bmatrix} z ​​\\ w \ end {bmatrix}} {\ begin {bmatrix} {\ bar {z}} & {\ bar {w}} \ end {bmatrix}}.

En resumen, la acción del grupo de Lorentz restringido SO ⁺ (1,3) concuerda con la del grupo de Möbius PSL (2, C ). Esto motiva la siguiente definición. En la dimensión n  ≥ 2, el grupo Möbius Möb ( n ) es el grupo de todas las isometrías conformes que conservan la orientación de la esfera redonda S ⁿ para sí mismo. Al realizar la esfera conforme como el espacio de los rayos que apuntan al futuro del cono nulo en el espacio R ^{1, n + 1 de}Minkowski , existe un isomorfismo de Möb ( n ) con el grupo de Lorentz restringido SO ⁺ (1, n+1) de las transformaciones de Lorentz con determinante positivo, preservando la dirección del tiempo.

Coxeter comenzó en cambio con la forma cuadrática equivalente. $${\ displaystyle Q (x_ {1}, \ x_ {2}, \ x_ {3} \ x_ {4}) = x_ {1} ^ {2} + x_ {2} ^ {2} + x_ {3} ^ {2} -x_ {4} ^ {2}.}

Identificó el grupo de Lorentz con transformaciones para las cuales { x  : Q ( x ) = -1} es estable . Luego interpretó las x como coordenadas homogéneas y { x  : Q ( x ) = 0}, el cono nulo , como el absoluto de Cayley para un espacio hiperbólico de puntos { x  : Q ( x ) <0 font="" nbsp="">A continuación, Coxeter introdujo las variables.

$${\ displaystyle \ xi = {\ frac {x_ {1}} {x_ {4}}}, \ \ eta = {\ frac {x_ {2}} {x_ {4}}}, \ \ zeta = {\ frac {x_ {3}} {x_ {4}}}}

de modo que el cuádrico invariante de Lorentz corresponde a la esfera $${\ displaystyle \ xi ^ {2} + \ eta ^ {2} + \ zeta ^ {2} = 1.}Coxeter señala que Felix Klein también escribió sobre esta correspondencia, aplicando una proyección estereográfica desde (0, 0, 1) al plano complejo.$${\ displaystyle z = {\ frac {\ xi + i \ eta} {1- \ zeta}}.} Coxeter utilizó el hecho de que los círculos del plano inverso representan planos del espacio hiperbólico, y la homografía general es el producto de las inversiones en dos o cuatro círculos, correspondiente al desplazamiento hiperbólico general que es el producto de las inversiones en dos o cuatro planos.

Espacio hiperbólico [ editar ]

Como se vio anteriormente, el grupo Möbius PSL (2, C ) actúa en el espacio Minkowski como el grupo de esas isometrías que preservan el origen, la orientación del espacio y la dirección del tiempo. La restricción a los puntos donde Q = 1 en el cono de luz positiva, que forman un modelo de hiperbólica 3-espacio H  ³ , vemos que el grupo de Möbius actúa sobre H  ³ como un grupo de isometrías conserva la orientación. De hecho, el grupo de Möbius es igual al grupo de isometrías que preservan la orientación del espacio 3 hiperbólico.