MECÁNICA CUÁNTICA

La fórmula SP para la tasa de desfase$${\ displaystyle \ Gamma _ {\ varphi}}Una partícula que se mueve en un entorno fluctuante unifica diversos resultados que se han obtenido, especialmente en la física de la materia condensada , con respecto al movimiento de los electrones en un metal. ^{[1] [2] [3] [4]} El caso general requiere tener en cuenta no solo las correlaciones temporales sino también las correlaciones espaciales de las fluctuaciones ambientales. ^[5] [6] Estos se pueden caracterizar por el factor de forma espectral$${\ displaystyle {\ tilde {S}} (q, \ omega)}, mientras que el movimiento de la partícula se caracteriza por su espectro de potencia. $${\ displaystyle {\ tilde {P}} (q, \ omega)}. En consecuencia, a una temperatura finita, la expresión para la tasa de desfase toma la siguiente forma que implica las funciones "S" y "P": ^{[7] [8] [9]}

$${\ displaystyle \ Gamma _ {\ varphi} \ = \ \ int d {q} \ int {\ frac {d \ omega} {2 \ pi}} \, {\ tilde {S}} ({q}, \ omega) \, {\ tilde {P}} (- {q}, - \ omega)}

Debido a las limitaciones inherentes de la aproximación semiclásica (fase estacionaria), el procedimiento físicamente correcto es utilizar las versiones cuánticas no simetrizadas de $${\ displaystyle {\ tilde {S}} (q, \ omega)} y $${\ displaystyle {\ tilde {P}} (q, \ omega)}. El argumento se basa en la analogía de la expresión anterior con el cálculo de la regla de oro de Fermi de las transiciones que son inducidas por la interacción sistema-entorno.

Derivación [ editar ]

Es muy ilustrativo entender la fórmula SP en el contexto del modelo DLD , que describe el movimiento en un desorden dinámico. Con el fin de derivar la fórmula de tasa de desfase a partir de los primeros principios, se puede adoptar una definición basada en la pureza del factor de desfase. ^[10] [11] La pureza$${\ displaystyle P (t) = e ^ {- F (t)}}describe cómo un estado cuántico se mezcla debido al enredo del sistema con el entorno. Usando la teoría de la perturbación, uno se recupera a temperaturas finitas en el límite de tiempo largo$${\ displaystyle F (t) = \ Gamma _ {\ varphi} t}, donde la constante de descomposición viene dada por la fórmula de tasa de desfase con funciones espectrales no simetrizadas como se esperaba. Existe una posibilidad un tanto controvertida de obtener la decadencia de la ley de poder$${\ displaystyle P (t)}en el límite de temperatura cero. ^[12] La forma adecuada de incorporar el bloqueo de Pauli en el cálculo de desfase de muchos cuerpos, ^{[13] también} se ha aclarado en el marco del enfoque de la fórmula SP. ^[14]

Ejemplo [ editar ]

Para el ambiente estándar 1D Caldeira-Leggett Ohmic, con temperatura $${\ displaystyle T} y fricción $${\ displaystyle \ eta}, el factor de forma espectral es

$${\ displaystyle {\ tilde {S}} (q, \ omega) \ = \ {\ frac {(2 \ pi) \ delta (q)} {q ^ {2}}} \, \ left [{\ frac {2 \ eta \ omega} {1-e ^ {- \ omega / T}}} \ right]}

Esta expresión refleja que en el límite clásico el electrón experimenta un "ruido temporal blanco", lo que significa una fuerza que no está correlacionada en el tiempo, pero uniforme es el espacio (alto $${\ displaystyle q}los componentes están ausentes). En contraste con eso, para el movimiento difusivo de un electrón en un entorno metálico 3D, que es creado por el resto de los electrones, el factor de forma espectral es

$${\ displaystyle {\ tilde {S}} (q, \ omega) \ = \ {\ frac {1} {\ nu Dq ^ {2}}} \ left [{\ frac {2 \ omega} {1-e ^ {- \ omega / T}}} \ right].}

Esta expresión refleja que en el límite clásico el electrón experimenta el "ruido espacio-temporal blanco", lo que significa una fuerza que no está correlacionada en el tiempo ni en el espacio. El espectro de potencia de un solo electrón difusivo es

$${\ displaystyle {\ tilde {P}} (q, \ omega) \ \ = \ \ {\ frac {2Dq ^ {2}} {\ omega ^ {2} + (Dq ^ {2}) ^ {2} }}}

Pero en el contexto de muchos cuerpos, esta expresión adquiere un "factor de bloqueo de Fermi":

$${\ displaystyle {\ tilde {P}} (q, \ omega) \ \ = \ \ {\ frac {d} {d \ omega}} \ left [{\ frac {\ omega} {1-e ^ {- \ omega / T}}} \ right] \ times {\ frac {2Dq ^ {2}} {\ omega ^ {2} + (Dq ^ {2}) ^ {2}}}}

Al calcular la integral SP obtenemos el conocido resultado. $${\ displaystyle \ Gamma _ {\ varphi} \ propto T ^ {3/2}}.

Hay muchas maneras de derivar las transformaciones de Lorentzutilizando una variedad de principios físicos, desde las ecuaciones de Maxwell hasta los postulados de Einstein de la relatividad especial y las herramientas matemáticas , que abarcan desde el álgebra elemental y las funciones hiperbólicas , hasta el álgebra lineal y la teoría de grupos .

Este artículo proporciona algunos de los más fáciles de seguir en el contexto de la relatividad especial , para el caso más simple de un refuerzo de Lorentz en la configuración estándar, es decir, dos marcos inerciales que se mueven entre sí a una velocidad relativaconstante (uniforme) menor que la velocidad de luz , y utilizando coordenadas cartesianas para que los ejes x y x 'sean colineales.

Transformación de Lorentz [ editar ]

Artículo principal: Transformación de Lorentz.

En las ramas fundamentales de la física moderna , es decir, la relatividad general y su subconjunto ampliamente aplicable la relatividad especial , así como la mecánica cuántica relativista y la teoría cuántica de campos relativista , la transformación de Lorentz es la regla de transformación en virtud del cual todos los cuatro vectoresy tensores que contienen cantidades físicas transforman De un marco de referencia a otro.

Los ejemplos principales de estos cuatro vectores son la posición cuatro y el impulso de una partícula , y para los campos el tensor electromagnético y el tensor de tensión-energía . El hecho de que estos objetos se transformen de acuerdo con la transformación de Lorentz es lo que matemáticamente los define como vectores y tensores; ver tensor para una definición.

Dadas las componentes de los cuatro vectores o tensores en algunos marcos, la "regla de transformación" permite determinar los componentes alterados de los mismos cuatro vectores o tensores en otros marcos, que podrían ser impulsados ​​o acelerados, en relación con el marco original. Un "impulso" no debe combinarse con la traducción espacial , sino que se caracteriza por la velocidad relativa entre los fotogramas. La propia regla de transformación depende del movimiento relativo de los cuadros. En el caso más simple de dos marcos inerciales,la velocidad relativa entre entra en la regla de transformación. Para marcos de referencia giratorios o marcos de referencia no inerciales generales, se necesitan más parámetros, incluida la velocidad relativa (magnitud y dirección), el eje de rotación y el ángulo girado.

Antecedentes históricos [ editar ]

El tratamiento habitual (p. Ej., El trabajo original de Einstein ) se basa en la invariancia de la velocidad de la luz. Sin embargo, este no es necesariamente el punto de partida: de hecho (como se expone, por ejemplo, en el segundo volumen del Curso de Física Teórica de Landau y Lifshitz ), lo que realmente está en juego es la localidad de las interacciones: se supone que la Influencia que una partícula, digamos, ejerce sobre otra, no puede ser transmitida instantáneamente. Por lo tanto, existe una velocidad máxima teórica de transmisión de información que debe ser invariable, y resulta que esta velocidad coincide con la velocidad de la luz en el vacío. Newtonél mismo llamó a la idea de acción a distancia filosóficamente "absurda", y sostuvo que la gravedad tenía que ser transmitida por algún agente de acuerdo con ciertas leyes. ^[1]

Michelson y Morley en 1887 diseñaron un experimento, empleando un interferómetro y un espejo semi plateado, que era lo suficientemente preciso para detectar el flujo de éter. El sistema de espejo reflejó la luz nuevamente dentro del interferómetro. Si hubiera una desviación del éter, se produciría un cambio de fase y un cambio en la interferencia que se detectaría. Sin embargo, nunca se encontró ningún cambio de fase. El resultado negativo del experimento de Michelson-Morley dejó el concepto de éter (o su deriva) socavado. Hubo una perplejidad consecuente en cuanto a por qué la luz se comporta como una onda, sin ningún medio detectable a través del cual la actividad de la onda podría propagarse.

En un artículo de 1964, ^[2] Erik Christopher Zeeman demostró que la propiedad de preservación de la causalidad, una condición que es más débil en sentido matemático que la invariancia de la velocidad de la luz, es suficiente para asegurar que las transformaciones de coordenadas sean las transformaciones de Lorentz. El artículo de Norman Goldstein muestra un resultado similar al usar la inercia (la preservación de las líneas temporales) en lugar de la causalidad . ^[3]

Principios físicos [ editar ]

Einstein basó su teoría de la relatividad especial en dos postulados fundamentales . Primero, todas las leyes físicas son las mismas para todos los marcos de referencia inerciales, independientemente de su estado relativo de movimiento; y segundo, la velocidad de la luz en el espacio libre es la misma en todos los marcos de referencia inerciales, de nuevo, independientemente de la velocidad relativa de cada marco de referencia. La transformación de Lorentz es fundamentalmente una consecuencia directa de este segundo postulado.

El segundo postulado [ editar ]

Supongamos el segundo postulado de la relatividad especial que indica la constancia de la velocidad de la luz, independientemente del marco de referencia, y considere una colección de sistemas de referencia que se mueven entre sí con velocidad constante, es decir , sistemas inerciales , cada uno dotado de su propio conjunto de cartesiano. Coordina el etiquetado de los puntos, es decir, eventos de espacio-tiempo. Para expresar la invariancia de la velocidad de la luz en forma matemática, arregle dos eventos en el espacio-tiempo, para que se registren en cada marco de referencia. Deje que el primer evento sea la emisión de una señal luminosa, y el segundo evento sea que se absorba.

Elija cualquier marco de referencia en la colección. En sus coordenadas, al primer evento se le asignarán las coordenadas.$${\ displaystyle x_ {1}, y_ {1}, z_ {1}, ct_ {1}}, y el segundo $${\ displaystyle x_ {2}, y_ {2}, z_ {2}, ct_ {2}}. La distancia espacial entre emisión y absorción es$${\ displaystyle {\ sqrt {(x_ {2} -x_ {1}) ^ {2} + (y_ {2} -y_ {1}) ^ {2} + (z_ {2} -z_ {1}) ^ {2}}}}, pero esta es también la distancia $${\ displaystyle c (t_ {2} -t_ {1})}Viajó por la señal. Por lo tanto, uno puede establecer la ecuación

$${\ displaystyle c ^ {2} (t_ {2} -t_ {1}) ^ {2} - (x_ {2} -x_ {1}) ^ {2} - (y_ {2} -y_ {1} ) ^ {2} - (z_ {2} -z_ {1}) ^ {2} = 0.}

Cada otro sistema de coordenadas registrará, en sus propias coordenadas, la misma ecuación. Esta es la consecuencia matemática inmediata de la invariancia de la velocidad de la luz. La cantidad a la izquierda se llama el intervalo espacio-tiempo . El intervalo es, para eventos separados por señales luminosas, el mismo (cero) en todos los cuadros de referencia, y por lo tanto se llama invariante .

Invarianza de intervalo [ editar ]

Para que la transformación de Lorentz tenga el significado físico realizado por la naturaleza, es crucial que el intervalo sea una medida invariante para cualquiera de los dos eventos, no solo para aquellos separados por señales de luz. Para establecer esto, se considera un intervalo infinitesimal , ^[4]

$${\ displaystyle ds ^ {2} = c ^ {2} dt ^ {2} -dx ^ {2} -dy ^ {2} -dz ^ {2},}

como se registra en un sistema $${\ displaystyle K}. Dejar$${\ displaystyle K '} Ser otro sistema asignando el intervalo. $${\ displaystyle ds '^ {2}}A los mismos dos eventos separados infinitesimalmente. Ya que si$${\ displaystyle ds ^ {2} = 0}, entonces el intervalo será nulo en cualquier otro sistema (segundo postulado), y desde $${\ displaystyle ds ^ {2}} y $${\ displaystyle ds '^ {2}} Son infinitesimales del mismo orden, deben ser proporcionales entre sí,

$${\ displaystyle ds ^ {2} = ads '^ {2}.}

En lo que pueda $${\ displaystyle a}¿depender? Puede que no dependa de las posiciones de los dos eventos en el espacio-tiempo, porque eso violaría la homogeneidad postulada del espacio-tiempo . Podría depender de la velocidad relativa$${\ displaystyle V '} Entre $${\ displaystyle K} y $${\ displaystyle K '}, pero solo en la velocidad, no en la dirección, porque esta última violaría la isotropía del espacio .

Ahora trae sistemas $${\ displaystyle K_ {1}} y $${\ displaystyle K_ {2}},

$${\ displaystyle ds ^ {2} = a (V_ {1}) ds_ {1} ^ {2}, \ quad ds ^ {2} = a (V_ {2}) ds_ {2} ^ {2}, \ quad ds_ {1} ^ {2} = a (V_ {12}) ds_ {2} ^ {2}.}

De estos se deduce,

$${\ displaystyle {\ frac {a (V_ {2})} {a (V_ {1})}} = a (V_ {12}).}

Ahora se observa que a la derecha, $${\ displaystyle V_ {12}} no solo depende de $${\ displaystyle V_ {1}} y $${\ displaystyle V_ {2}}, pero también en el ángulo entre los vectores $${\ displaystyle {\ textbf {V}} _ {1}} y $${\ displaystyle {\ textbf {V}} _ {2}}. El lado izquierdo no depende de este ángulo, y la única manera de que la ecuación se mantenga verdadera es si la función$${\ displaystyle a (V)}es una constante, y por la misma ecuación esta constante es la unidad. Así,

$${\ displaystyle ds ^ {2} = ds '^ {2}}

para todos los sistemas $${\ displaystyle K '}, y como esto se mantiene para todos los intervalos infinitesimales, se mantiene para todos los intervalos. La mayoría, si no todas, las derivaciones de las transformaciones de Lorentz dan esto por sentado, y usan la constancia de la velocidad de la luz (invarianza de eventos separados similares a la luz) solamente. Este resultado asegura que la transformación de Lorentz sea la transformación correcta.

Configuración estándar [ editar ]

Las coordenadas espaciotemporales de un evento, según lo medido por cada observador en su marco de referencia inercial (en la configuración estándar) se muestran en las burbujas de discurso. 
Top: Marco F 'se mueve a la velocidad v a lo largo de la x eje x del bastidor F . 
Abajo: el cuadro F se mueve a la velocidad - v a lolargo del eje x 'del cuadro F '. ^[5]

El intervalo invariante se puede ver como una función de distancia definida no positiva en el espacio-tiempo. El conjunto de transformaciones buscadas debe dejar esta distancia invariante. Debido a la naturaleza cartesiana del sistema de coordenadas del marco de referencia, se concluye que, como en el caso de Euclides, las posibles transformaciones se componen de traslaciones y rotaciones, en las que debería permitirse un significado un poco más amplio para el término rotación.

El intervalo es bastante invariable trivialmente en la traducción. Para rotaciones, hay cuatro coordenadas. Por eso hay seis planos de rotación. Tres de ellas son rotaciones en planos espaciales. El intervalo es invariante también en las rotaciones ordinarias. ^[4]

Queda por encontrar una "rotación" en los tres planos de coordenadas restantes que dejan el intervalo invariante. De manera equivalente, para encontrar una forma de asignar coordenadas de modo que coincidan con las coordenadas correspondientes a un marco en movimiento.

El problema general es encontrar una transformación tal que

{\ displaystyle {\ begin {alineado} & \, \, \, \, \, \, \, \, c ^ {2} (t_ {2} -t_ {1}) ^ {2} - (x_ { 2} -x_ {1}) ^ {2} - (y_ {2} -y_ {1}) ^ {2} - (z_ {2} -z_ {1}) ^ {2} \\ & = c ^ {2} (t_ {2} '- t_ {1}') ^ {2} - (x_ {2} '- x_ {1}') ^ {2} - (y_ {2} '- y_ {1} ') ^ {2} - (z_ {2}' - z_ {1} ') ^ {2}. \ End {alineado}}}

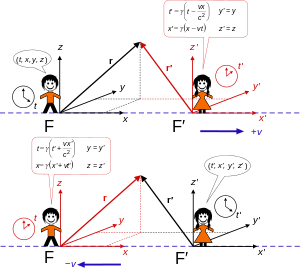
Para resolver el problema general, uno puede usar el conocimiento sobre la invariancia del intervalo de traslaciones y las rotaciones ordinarias para asumir, sin pérdida de generalidad, ^[4] que los cuadros F y F ' están alineados de tal manera que sus ejes de coordenadas están todos alineados. reúnase en t = t '= 0 y que los ejes x y x ' están alineados permanentemente y el sistema F ' tiene velocidad V a lo largo del eje x positivo . Llama a esto la configuración estándar . Reduce el problema general para encontrar una transformación tal que

$${\ displaystyle c ^ {2} (t_ {2} -t_ {1}) ^ {2} - (x_ {2} -x_ {1}) ^ {2} = c ^ {2} (t_ {2} '-t_ {1}') ^ {2} - (x_ {2} '- x_ {1}') ^ {2}.}

La configuración estándar se utiliza en la mayoría de los ejemplos a continuación. Cabe señalar que una solución lineal del problema más simple

$${\ displaystyle c ^ {2} t ^ {2} -x ^ {2} = c ^ {2} t '^ {2} -x' ^ {2}}

resuelve el problema más general ya que las diferencias de coordenadas se transforman de la misma manera. La linealidad se suele asumir o argumentar de alguna manera en la literatura cuando se considera este problema más simple. Si la solución al problema más simple no es lineal, entonces no resuelve el problema original debido a los términos cruzados que aparecen al expandir los cuadrados.

Las soluciones [ editar ]

Como se mencionó, el problema general se resuelve con las traducciones en el espacio-tiempo. Estos no aparecen como una solución al problema más simple planteado, mientras que los incrementos sí (y algunas veces las rotaciones dependen del ángulo de ataque). Incluso existen más soluciones si uno solo insiste en la invariancia del intervalo para eventos separados similares a la luz. Estas son transformaciones conformes no lineales ("preservación de ángulo"). Uno tiene

Transformaciones de Lorentz ⊂ Poincaré transformaciones ⊂ transformaciones de grupos de conformación .

Algunas ecuaciones de la física son invariantes conformes, por ejemplo, las ecuaciones de Maxwell en el espacio sin fuente, ^[6] pero no todas. La relevancia de las transformaciones conformales en el espacio-tiempo no se conoce en la actualidad, pero el grupo conformal en dos dimensiones es altamente relevante en la teoría de campos conformes y la mecánica estadística . ^{[7] Así} , es el grupo de Poincaré el que se destaca por los postulados de la relatividad especial. Es la presencia de impulsos de Lorentz (para los cuales la adición de velocidad es diferente de la simple adición de vectores que permitiría velocidades mayores que la velocidad de la luz) en oposición a los impulsos ordinarios que lo separa del grupo de GalileoLa relatividad galileana . Las rotaciones espaciales, las inversiones espaciales y temporales y las traducciones están presentes en ambos grupos y tienen las mismas consecuencias en ambas teorías (leyes de conservación del momento, la energía y el momento angular). No todas las teorías aceptadas respetan la simetría en las inversiones.

Usando la geometría del espacio-tiempo [ editar ]

Solución de Landau y Lifshitz [ editar ]

espectáculo

Tres fórmulas útiles de función hiperbólica (H1-H3).

El problema planteado en la configuración estándar para un aumento en la dirección x , donde las coordenadas imprimadas se refieren al sistema en movimiento , se resuelve encontrando una solución lineal para el problema más simple

$${\ displaystyle c ^ {2} t ^ {2} -x ^ {2} = c ^ {2} t '^ {2} -x' ^ {2}.}

La solución más general es, como puede verificarse mediante sustitución directa utilizando (H1), ^[4]

$${\ displaystyle x = x '\ cosh \ Psi + ct' \ sinh \ Psi, \ quad ct = x '\ sinh \ Psi + ct' \ cosh \ Psi.}

( 1 )

Para encontrar el rol de Ψ en la configuración física, registre el origen de la progresión de F ' , es decir, x ' = 0, x = vt . Las ecuaciones se convierten (usando la primera x '= 0 ),

$${\ displaystyle x = ct '\ sinh \ Psi, \ quad ct = ct' \ cosh \ Psi.}

Ahora divide:

$${\ displaystyle {\ frac {x} {ct}} = \ tanh \ Psi = {\ frac {v} {c}} \ Rightarrow \ quad \ sinh \ Psi = {\ frac {\ frac {v} {c} } {\ sqrt {1 - {\ frac {v ^ {2}} {c ^ {2}}}}}}, \ quad \ cosh \ Psi = {\ frac {1} {\ sqrt {1 - {\ frac {v ^ {2}} {c ^ {2}}}}}},}

donde x = vt se utilizó en el primer paso, (H2) y (H3) en el segundo, que, cuando se enchufa de nuevo en (1) , da

$${\ displaystyle x = {\ frac {x '+ vt'} {\ sqrt {1 - {\ frac {v ^ {2}} {c ^ {2}}}}}}, \ quad t = {\ frac {t '+ {\ frac {v} {c ^ {2}}} x'} {\ sqrt {1 - {\ frac {v ^ {2}} {c ^ {2}}}}}},}

o, con las abreviaturas habituales,

$${\ displaystyle x = \ gamma (x '+ vt'), \, \, t = \ gamma \ left (t '+ {\ frac {vx'} {c ^ {2}}} \ right), \ quad x '= \ gamma (x-vt), \, \, t' = \ gamma \ left (t - {\ frac {vx} {c ^ {2}}} \ right).

Este cálculo se repite con más detalle en la sección rotación hiperbólica .

La rotación hiperbólica [ editar ]

Artículo principal: Rotación hiperbólica.

Las transformaciones de Lorentz también pueden derivarse mediante la simple aplicación de los postulados de la relatividad especial y el uso de identidades hiperbólicas . ^[8]

Postulados de la relatividad.

Comience con las ecuaciones del frente de onda esférica de un pulso de luz, centrado en el origen:

$${\ displaystyle (ct) ^ {2} - (x ^ {2} + y ^ {2} + z ^ {2}) = (ct ') ^ {2} - (x' ^ {2} + y ' ^ {2} + z '^ {2}) = 0}

que toman la misma forma en ambos marcos debido a los postulados de la relatividad especial. A continuación, considere el movimiento relativo a lo largo de los x ejes de cada cuadro, en la configuración estándar anterior, de modo que y = y ′, z = z ′, que se simplifica a

$${\ displaystyle (ct) ^ {2} -x ^ {2} = (ct ') ^ {2} -x' ^ {2}}

Linealidad

Ahora asume que las transformaciones toman la forma lineal:

{\ displaystyle {\ begin {alineado} x '& = Axe + Bct \\ ct' & = Cx + Dct \ end {alineado}}}

donde A , B , C , D se encuentran. Si no fueran lineales, no tomarían la misma forma para todos los observadores, ya que las fuerzas ficticias (por lo tanto, las aceleraciones) ocurrirían en un cuadro, incluso si la velocidad fuera constante en otro, lo que es inconsistente con las transformaciones del marco inercial. ^[9]

Sustituyendo en el resultado anterior:

$${\ displaystyle (ct) ^ {2} -x ^ {2} = [(Cx) ^ {2} + (Dct) ^ {2} + 2CDcxt] - [(Ax) ^ {2} + (Bct) ^ {2} + 2ABcxt]}

y comparando los coeficientes de x ² , t ² , xt :

{\ displaystyle {\ begin {alineado} -1 = C ^ {2} -A ^ {2} & \ Rightarrow & A ^ {2} -C ^ {2} = 1 \\ c ^ {2} = (Dc) ^ {2} - (Bc) ^ {2} & \ Rightarrow & D ^ {2} -B ^ {2} = 1 \\ 2CDc-2ABc = 0 & \ Rightarrow & AB = CD \ end {alineado}}}

Rotación hiperbólica

Las ecuaciones sugieren la identidad hiperbólica. $${\ displaystyle \ cosh ^ {2} \ phi - \ sinh ^ {2} \ phi = 1.}

La introducción del parámetro de rapidez ϕ como un ángulo hiperbólico permite las identificaciones consistentes

$${\ displaystyle A = D = \ cosh \ phi \ ,, \ quad C = B = - \ sinh \ phi}

donde se eligen los signos después de las raíces cuadradas para que x y t aumenten. Las transformaciones hiperbólicas se han resuelto para:

{\ displaystyle {\ begin {alineado} x '& = x \ cosh \ phi -ct \ sinh \ phi \\ ct' & = - x \ sinh \ phi + ct \ cosh \ phi \ end {alineado}}}

Si los signos se eligieran de forma diferente, las coordenadas de posición y tiempo deberían reemplazarse por - xy / o - t para que x y t no aumenten.

Para encontrar cómo ϕ se relaciona con la velocidad relativa, desde la configuración estándar, el origen del cuadro imprimado x ′ = 0 se mide en el cuadro no imprimido para que sea x = vt (o la ronda equivalente y opuesta; el origen del cuadro no imprimido es x = 0 y en el cuadro preparado se encuentra en x ′ = - vt ):

$${\ displaystyle 0 = vt \ cosh \ phi -ct \ sinh \ phi \, \ Rightarrow \, \ tanh \ phi = {\ frac {v} {c}} = \ beta}

y la manipulación de las identidades hiperbólicas lleva a las relaciones entre β , γ y ϕ ,

$${\ displaystyle \ cosh \ phi = \ gamma, \, \ quad \ sinh \ phi = \ beta \ gamma \ ,.}

De los principios físicos [ editar ]

El problema generalmente se limita a dos dimensiones mediante el uso de una velocidad a lo largo de la x eje de tal manera que las Y y Z coordenadas no intervienen, como se describe en configuración estándar anteriormente.

La dilatación del tiempo y la contracción de la longitud [ editar ]

Las ecuaciones de transformación se pueden derivar de la dilatación del tiempo y la contracción de la longitud , que a su vez se pueden derivar de los primeros principios. Con O y O ′ que representan los orígenes espaciales de los cuadros F y F ′ , y algún evento M , la relación entre los vectores de posición (que aquí se reducen a los segmentos orientados OM , OO ′ y O′M ) en ambos cuadros viene dada por : ^[10]

OM = OO ′ + O′M .

Usando las coordenadas ( x, t ) en F y ( x ′, t ′ ) en F ′ para el evento M, en el cuadro F los segmentos son OM = x , OO ′ = vt y O′M = x ′ / γ (ya que x ′ Es O′M como se mide en F ′ ):

$${\ displaystyle x = vt + x '/ \ gamma.}

Del mismo modo, en el cuadro F ′ , los segmentos son OM = x / γ (ya que x es OM como se mide en F ), OO ′ = vt ′ y O′M = x ′ :

$${\ displaystyle x / \ gamma = vt '+ x'.}

Al reorganizar la primera ecuación, obtenemos

$${\ displaystyle x '= \ gamma (x-vt),}

que es la parte espacial de la transformación de lorentz. La segunda relación da.

$${\ displaystyle x = \ gamma (x '+ vt'),}

que es la inversa de la parte espacial. Eliminando x ′ entre las dos ecuaciones de la parte del espacio da

$${\ displaystyle t '= \ gamma (t-vx / c ^ {2}),}

que es la parte temporal de la transformación, cuya inversa se encuentra por una eliminación similar de x :

$${\ displaystyle t = \ gamma (t '+ vx' / c ^ {2}).}

Ondas esféricas de luz [ editar ]

Lo siguiente es similar al de Einstein. ^[11] [12] Al igual que en la transformación de Galilea , la transformación de Lorentz es lineal ya que la velocidad relativa de los marcos de referencia es constante como un vector; De lo contrario, aparecerían fuerzas inerciales . Se denominan marcos de referencia inerciales o galileanos. Según la relatividad ningún marco de referencia galileo es privilegiado. Otra condición es que la velocidad de la luz debe ser independiente del marco de referencia, en la práctica de la velocidad de la fuente de luz.

Considere dos marcos de referencia inerciales O y O ', suponiendo que O está en reposo mientras O ' se mueve con una velocidad v con respecto a O en la dirección x positiva . Los orígenes de O y O ′ inicialmente coinciden entre sí. Una señal luminosa se emite desde el origen común y viaja como un frente de onda esférico. Considere un punto P en un frente de onda esférico a una distancia r y r ′ de los orígenes de O y O′ Respectivamente. De acuerdo con el segundo postulado de la teoría especial de la relatividad, la velocidad de la luz es la misma en ambos cuadros, así que para el punto P :

{\ displaystyle {\ begin {alineado} r & = ct \\ r '& = ct'. \ end {alineado}}}

La ecuación de una esfera en el cuadro O está dada por

$${\ displaystyle x ^ {2} + y ^ {2} + z ^ {2} = r ^ {2}.}

Por el frente de onda esférico que se convierte

$${\ displaystyle x ^ {2} + y ^ {2} + z ^ {2} = c ^ {2} t ^ {2}.}

De manera similar, la ecuación de una esfera en el cuadro O ′ está dada por

$${\ displaystyle x '^ {2} + y' ^ {2} + z '^ {2} = r' ^ {2},}

así que el frente de onda esférico satisface

$${\ displaystyle x '^ {2} + y' ^ {2} + z '^ {2} = c ^ {2} t' ^ {2}.}

El origen O ′ se está moviendo a lo largo del eje x . Por lo tanto,

{\ displaystyle {\ begin {alineado} y '& = y \\ z' & = z. \ end {alineado}}}

x 'debe variar linealmente con x y t . Por lo tanto, la transformación tiene la forma.

$${\ displaystyle x '= \ gamma x + \ sigma t.}

Para el origen de O ′ x ' y x están dados por

{\ displaystyle {\ begin {alineado} x '& = 0 \\ x & = vt, \ end {alineado}}}

así, para todo t ,

$${\ displaystyle 0 = \ gamma vt + \ sigma t}

y por lo tanto

$${\ displaystyle \ sigma = - \ gamma v.}

Esto simplifica la transformación a

$${\ displaystyle x '= \ gamma \ left (x-vt \ right)}

donde γ se va a determinar. En este punto, γ no es necesariamente una constante, pero se requiere que se reduzca a 1 para v ≪ c .

La transformación inversa es la misma, excepto que el signo de v se invierte:

$${\ displaystyle x = \ gamma \ left (x '+ vt' \ right).}

Las dos ecuaciones anteriores dan la relación entre t y t ′ como:

$${\ displaystyle x = \ gamma \ left [\ gamma \ left (x-vt \ right) + vt '\ right]}

o

$${\ displaystyle t '= \ gamma t + {\ frac {\ left (1 - {\ gamma ^ {2}} \ right) x} {\ gamma v}}.}

Reemplazando x ′, y ′, z ′ y t ′ en la ecuación de frente de onda esférica en el cuadro O ′,

$${\ displaystyle x '^ {2} + y' ^ {2} + z '^ {2} = c ^ {2} t' ^ {2},}

con sus expresiones en términos de x , y , z y t produce:

$${\ displaystyle {\ gamma ^ {2}} \ left (x-vt \ right) ^ {2} + y ^ {2} + z ^ {2} = c ^ {2} \ left [\ gamma t + {\ frac {\ left (1 - {\ gamma ^ {2}} \ right) x} {\ gamma v}} \ right] ^ {2}}

y por lo tanto,

$${\ displaystyle \ gamma ^ {2} x ^ {2} + \ gamma ^ {2} v ^ {2} t ^ {2} -2 \ gamma ^ {2} vtx + y ^ {2} + z ^ { 2} = c ^ {2} {\ gamma ^ {2}} t ^ {2} + {\ frac {\ left (1 - {\ gamma ^ {2}} \ right) ^ {2} c ^ {2 } x ^ {2}} {{\ gamma ^ {2}} v ^ {2}}} + 2 {\ frac {\ left (1 - {\ gamma ^ {2}} \ right) txc ^ {2} } {v}}}

lo que implica,

$${\ displaystyle \ left [{\ gamma ^ {2}} - {\ frac {\ left (1 - {\ gamma ^ {2}} \ right) ^ {2} c ^ {2}} {{\ gamma ^ {2}} v ^ {2}}} \ right] x ^ {2} -2 {\ gamma ^ {2}} vtx + y ^ {2} + z ^ {2} = \ left (c ^ {2 } {\ gamma ^ {2}} - v ^ {2} {\ gamma ^ {2}} \ derecha) t ^ {2} +2 {\ frac {\ left [1 - {\ gamma ^ {2}} \ right] txc ^ {2}} {v}}}

o

$${\ displaystyle \ left [{\ gamma ^ {2}} - {\ frac {\ left (1 - {\ gamma ^ {2}} \ right) ^ {2} c ^ {2}} {{\ gamma ^ {2}} v ^ {2}}} \ derecha] x ^ {2} - \ izquierda [2 {\ gamma ^ {2}} v + 2 {\ frac {\ izquierda (1 - {\ gamma ^ {2 }} \ derecha) c ^ {2}} {v}} \ derecha] tx + y ^ {2} + z ^ {2} = \ izquierda [c ^ {2} {\ gamma ^ {2}} - v ^ {2} {\ gamma ^ {2}} \ right] t ^ {2}}

La comparación del coeficiente de t ² en la ecuación anterior con el coeficiente de t ² en la ecuación de frente de onda esférica para el cuadro O produce:

$${\ displaystyle c ^ {2} {\ gamma ^ {2}} - v ^ {2} {\ gamma ^ {2}} = c ^ {2}}

Las expresiones equivalentes para γ se pueden obtener haciendo coincidir los coeficientes x ² o estableciendo el coeficiente tx a cero. Reorganizar

$${\ displaystyle {\ gamma ^ {2}} = {\ frac {1} {1 - {\ frac {v ^ {2}} {c ^ {2}}}}}}

o, eligiendo la raíz positiva para asegurar que los ejes x y x 'y los ejes de tiempo apuntan en la misma dirección,

$${\ displaystyle {\ gamma} = {\ frac {1} {\ sqrt {1 - {\ frac {v ^ {2}} {c ^ {2}}}}}}

que se llama el factor de lorentz . Esto produce la transformación de Lorentz a partir de la expresión anterior. Es dado por

{\ displaystyle {\ begin {alineado} x '& = \ gamma \ left (x-vt \ right) \\ t' & = \ gamma \ left (t - {\ frac {vx} {c ^ {2}} } \ right) \\ y '& = y \\ z' & = z \ end {alineado}}}

La transformación de Lorentz no es la única transformación que deja invariante la forma de las ondas esféricas, ya que hay un conjunto más amplio de transformaciones de ondas esféricas en el contexto de la geometría conformal , dejando invariante la expresión$${\ displaystyle \ lambda \ left (\ delta x ^ {2} + \ delta y ^ {2} + \ delta z ^ {2} -c ^ {2} \ delta t ^ {2} \ right)}. Sin embargo, las transformaciones conformes de cambio de escala no pueden usarse para describir simétricamente todas las leyes de la naturaleza, incluida la mecánica , mientras que las transformaciones de Lorentz (la única que implica$${\ displaystyle \ lambda = 1}) representan una simetría de todas las leyes de la naturaleza y se reducen a las transformaciones de Galilea en $${\ displaystyle v \ ll c}.

Galileo y la relatividad de Einstein [ editar ]

Marcos de referencia galileanos [ editar ]

En cinemática clásica, el desplazamiento total x en el cuadro R es la suma del desplazamiento relativo x ′ en el cuadro R ′ y de la distancia entre los dos orígenes x - x ′. Si v es la velocidad relativa de R ′ relativa a R, la transformación es: x  =  x ′ +  vt , o x ′ =  x  -  vt . Esta relación es lineal para una constante v , es decir, cuando Ry R ′ son marcos de referencia galileanos.

En la relatividad de Einstein, la principal diferencia con la relatividad galileana es que las coordenadas de espacio y tiempo están entrelazadas, y en diferentes marcos inerciales t  ≠  t ′.

Dado que se supone que el espacio es homogéneo, la transformación debe ser lineal. La relación lineal más general se obtiene con cuatro coeficientes constantes, A , B , γ yb :

$${\ displaystyle x '= \ gamma x + bt \,}

$${\ displaystyle t '= Ax + Bt. \,}

La transformación de Lorentz se convierte en la transformación galileana cuando γ = B = 1, b = - v y A = 0.

Un objeto en reposo en el cuadro R ′ en la posición x ′ = 0 se mueve con velocidad constante v en el cuadro R. Por lo tanto, la transformación debe producir x ′ = 0 si x = vt . Por lo tanto, b = - γv y la primera ecuación se escribe como

$${\ displaystyle x '= \ gamma (x-vt) \ ,.}

Utilizando el principio de la relatividad [ editar ]

De acuerdo con el principio de relatividad, no hay un marco de referencia galileano privilegiado: por lo tanto, la transformación inversa para la posición del cuadro R 'al cuadro R debe tener la misma forma que el original pero con la velocidad en la dirección opuesta, ahora sustituyendo v con -v :

$${\ displaystyle x = \ gamma \ left (x '- (- v) t' \ right),}

y por lo tanto

$${\ displaystyle x = \ gamma \ left (x '+ vt' \ right).}

Determinando las constantes de la primera ecuación [ editar ]

Dado que la velocidad de la luz es la misma en todos los cuadros de referencia, para el caso de una señal luminosa, la transformación debe garantizar que t  =  x / c cuando t ′ =  x ′ / c .

Sustituir t y t ′ en las ecuaciones anteriores da:

$${\ displaystyle x '= \ gamma \ left (1-v / c \ right) x,}

$${\ displaystyle x = \ gamma \ left (1 + v / c \ right) x '.}

Multiplicando estas dos ecuaciones juntas da,

$${\ displaystyle xx '= \ gamma ^ {2} \ left (1-v ^ {2} / c ^ {2} \ right) xx'.}

En cualquier momento después de t = t ′ = 0, xx ′ no es cero, por lo que al dividir ambos lados de la ecuación por xx ′, se obtiene

$${\ displaystyle \ gamma = {\ frac {1} {\ sqrt {1 - {\ frac {v ^ {2}} {c ^ {2}}}}},}

que se llama el "factor de Lorentz".

Cuando se requieren las ecuaciones de transformación para satisfacer las ecuaciones de señal de luz en la forma x  =  ct y x ′ = ct ′, sustituyendo los valores de x y x '  , la misma técnica produce la misma expresión para el factor de Lorentz. ^[13] [14]

Determinando las constantes de la segunda ecuación [ editar ]

La ecuación de transformación para el tiempo se puede obtener fácilmente considerando el caso especial de una señal luminosa, que satisface nuevamente x  =  ct y x ′ =  ct ′, al sustituir término por término en la ecuación obtenida anteriormente por la coordenada espacial

$${\ displaystyle x '= \ gamma (x-vt), \,}

dando

$${\ displaystyle ct '= \ gamma \ left (ct - {\ frac {v} {c}} x \ derecha),}

así que eso

$${\ displaystyle t '= \ gamma \ left (t - {\ frac {v} {c ^ {2}}} x \ right),

el cual, cuando se identifica con

$${\ displaystyle t '= Ax + Bt, \,}

determina los coeficientes de transformación A y B como

$${\ displaystyle A = - \ gamma v / c ^ {2}, \,}

$${\ displaystyle B = \ gamma. \,}

Entonces, A y B son los coeficientes constantes únicos necesarios para preservar la constancia de la velocidad de la luz en el sistema de coordenadas cebado.

Derivación popular de Einstein [ editar ]

En su libro popular ^[15], Einstein derivó la transformación de Lorentz argumentando que debe haber dos constantes de acoplamiento no nulas λ y μ tales que

$${\ displaystyle {\ begin {cases} x'-ct '= \ lambda \ left (x-ct \ right) \\ x' + ct '= \ mu \ left (x + ct \ right) \, \ end { casos}}}

que corresponden a la luz que viaja a lo largo del eje x positivo y negativo, respectivamente. Para la luz x = ct si y solo si x ′ = ct ′ . Sumando y restando las dos ecuaciones y definiendo

$${\ displaystyle {\ begin {cases} \ gamma = \ left (\ lambda + \ mu \ right) / 2 \\ b = \ left (\ lambda - \ mu \ right) / 2, \, \ end {cases} }}

da

$${\ displaystyle {\ begin {cases} x '= \ gamma x-bct \\ ct' = \ gamma ct-bx. \, \ end {cases}}}

Sustituyendo x ′ = 0 correspondiente a x = vt y notando que la velocidad relativa es v = bc / γ , esto da

$${\ displaystyle {\ begin {cases} x '= \ gamma \ left (x-vt \ right) \\ t' = \ gamma \ left (t - {\ frac {v} {c ^ {2}}} x \ right) \, \ end {cases}}}

La constante γ puede evaluarse exigiendo c ² t ² - x ² = c ² t ' ² - x ' ² según la configuración estándar .