MECÁNICA CUÁNTICA

potencial delta es un potencial bien descrito matemáticamente por la función delta de Dirac , una función generalizada. Cualitativamente, corresponde a un potencial que es cero en todas partes, excepto en un solo punto, donde toma un valor infinito. Esto se puede usar para simular situaciones en las que una partícula es libre de moverse en dos regiones del espacio con una barrera entre las dos regiones. Por ejemplo, un electrón puede moverse casi libremente en un material conductor, pero si dos superficies conductoras se juntan, la interfaz entre ellas actúa como una barrera para el electrón que puede aproximarse mediante un potencial delta.

El pozo delta del potencial es un caso limitante del pozo de potencial finito , que se obtiene si se mantiene el producto del ancho del pozo y el potencial constante mientras se reduce el ancho del pozo y se aumenta el potencial.

Este artículo, por simplicidad, solo considera un potencial unidimensional, pero el análisis podría ampliarse a más dimensiones.

Potencial delta único [ editar ]

La ecuación de Schrödinger independiente del tiempo para la función de onda ψ ( x ) de una partícula en una dimensión en un potencial V ( x )es

$${\ displaystyle - {\ frac {\ hbar ^ {2}} {2m}} {\ frac {d ^ {2} \ psi} {dx ^ {2}}} (x) + V (x) \ psi ( x) = E \ psi (x) ~,}

donde ħ es la constante de Planck reducida y E es la energía de la partícula.

El potencial delta es el potencial.

$${\ displaystyle \ displaystyle V (x) = \ lambda \ delta (x) ~,}

donde δ ( x ) es la función delta de Dirac .

Se llama pozo de delta potencial si λ es negativo y barrera de potencial delta si λ es positivo. El delta ha sido definido para que ocurra en el origen por simplicidad; un cambio en el argumento de la función delta no cambia ninguno de los resultados del procedimiento.

Resolviendo la ecuación de Schrödinger [ editar ]

El potencial divide el espacio en dos partes ( x  <0 font="" nbsp="" y="">x  > 0). En cada una de estas partes, la energía potencial es cero, y la ecuación de Schrödinger se reduce a

$${\ displaystyle {\ frac {d ^ {2} \ psi} {dx ^ {2}}} = - {\ frac {2mE} {\ hbar ^ {2}}} \ psi ~;}

esta es una ecuación diferencial lineal con coeficientes constantes cuyas soluciones son combinaciones linealesde e ^ikx y e ^- ikx , donde el número de onda k está relacionado con la energía por

$${\ displaystyle k = {\ frac {\ sqrt {2mE}} {\ hbar}} ~.}

En general, debido a la presencia del potencial delta en el origen, los coeficientes de la solución no tienen que ser los mismos en los dos espacios intermedios:

{\ displaystyle \ psi (x) = {\ begin {cases} \ psi _ {\ mathrm {L}} (x) = A _ {\ mathrm {r}} e ^ {ikx} + A _ {\ mathrm {l} } e ^ {- ikx}, & {\ text {if}} x <0 _="" amp="" b="" e="" if="" ikx="" l="" mathrm="" psi="" r="" text="" x=""> 0, \ end {cases}}}

donde, en el caso de las energías positivas ( k real ), e ^ikx representa una onda que viaja hacia la derecha, y e ^- ikx una que viaja hacia la izquierda.

Uno obtiene una relación entre los coeficientes al imponer que la función de onda sea continua en el origen,

$${\ displaystyle \ psi (0) = \ psi _ {L} (0) = \ psi _ {R} (0) = A_ {r} + A_ {l} = B_ {r} + B_ {l} ~, }

Se puede encontrar una segunda relación estudiando la derivada de la función de onda. Normalmente, también podríamos imponer diferenciabilidad en el origen, pero esto no es posible debido al potencial delta. Sin embargo, si integramos la ecuación de Schrödinger alrededor de x  = 0, en un intervalo [- ε , + ε ]:

$${\ displaystyle - {\ frac {\ hbar ^ {2}} {2m}} \ int _ {- \ epsilon} ^ {+ \ epsilon} \ psi '' (x) \, dx + \ int _ {- \ epsilon } ^ {+ \ epsilon} V (x) \ psi (x) \, dx = E \ int _ {- \ epsilon} ^ {+ \ epsilon} \ psi (x) \, dx.}

En el límite como ε  → 0, el lado derecho de esta ecuación se desvanece; el lado izquierdo se convierte en

$${\ displaystyle \ textstyle - {\ frac {\ hbar ^ {2}} {2m}} [\ psi '_ {R} (0) - \ psi' _ {L} (0)] + \ lambda \ psi ( 0),}

porque

$${\ displaystyle \ int _ {- \ epsilon} ^ {+ \ epsilon} \ psi '' (x) \, dx = [\ psi '({+ \ epsilon}) - \ psi' ({- \ epsilon}) ].}

Sustituyendo la definición de ψ en esta expresión, se obtiene

$${\ displaystyle - {\ frac {\ hbar ^ {2}} {2m}} ik (-A_ {r} + A_ {l} + B_ {r} -B_ {l}) + \ lambda (A_ {r} + A_ {l}) = 0 ~.}

Las condiciones de contorno dan así las siguientes restricciones sobre los coeficientes.

{\ displaystyle {\ begin {cases} A_ {r} + A_ {l} -B_ {r} -B_ {l} & = 0; \\ - A_ {r} + A_ {l} + B_ {r} - B_ {l} & = {\ frac {2m \ lambda} {ik \ hbar ^ {2}}} (A_ {r} + A_ {l}) ~. \ End {cases}}}

Estado límite (E <0 nbsp="" span="">[ editar ]

La gráfica de la solución de la función de onda de estado unido al potencial de la función delta es continua en todas partes, pero su derivada no está definida en x = 0 .

En cualquier potencial atractivo unidimensional habrá un estado límite . Para encontrar su energía, tenga en cuenta que para E  <0 font="" nbsp="">k  =  i √ 2 m | E | / ħ  =  iκ es imaginario y las funciones de onda que oscilaban para energías positivas en el cálculo anterior, ahora son funciones exponenciales de aumento o disminución de x (ver arriba). Requerir que las funciones de onda no divergan al infinito elimina la mitad de los términos: A _r  = B _l  = 0. La función de onda es entonces

{\ displaystyle \ psi (x) = {\ begin {cases} \ psi _ {\ text {L}} (x) = A_ {l} e ^ {\ kappa x}, & {\ text {if}} x <0 _="" amp="" b_="" e="" if="" kappa="" psi="" r="" text="" x=""> 0. \ end {cases}} }

De las condiciones de contorno y las condiciones de normalización, se deduce que

$${\ displaystyle {\ begin {cases} A_ {l} = B_ {r} = {\ sqrt {\ kappa}}; \\\ kappa = - {\ frac {m \ lambda} {\ hbar ^ {2}} } ~; \ end {cases}}}

de lo cual se deduce que λ debe ser negativo, es decir, el estado límite solo existe para el pozo, y no para la barrera. La transformada de Fourier de esta función de onda es una función lorentziana .

La energía del estado ligado es entonces.

$${\ displaystyle E = - {\ frac {\ hbar ^ {2} \ kappa ^ {2}} {2m}} = - {\ frac {m \ lambda ^ {2}} {2 \ hbar ^ {2}} }.}

Dispersión (E> 0) [ editar ]

Probabilidad de transmisión (T) y reflexión (R) de un pozo de potencial delta. La energía E > 0 está en unidades de$${\ displaystyle {\ frac {m \ lambda ^ {2}} {2 \ hbar ^ {2}}} \, \!}. Punteado: resultado clásico. Línea continua: mecánica cuántica.

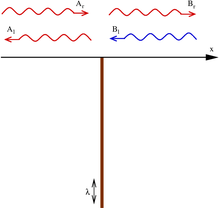
Para las energías positivas, la partícula puede moverse libremente en la mitad del espacio: x  <0 font="" o="">x  > 0. Puede estar dispersa en el potencial de la función delta.

El caso cuántico se puede estudiar en la siguiente situación: una partícula incidente en la barrera desde el lado izquierdo ( A _r ) . Puede ser reflejado( A _l ) o transmitido ( B _r ) . Para encontrar las amplitudes para la reflexión y la transmisión para la incidencia desde la izquierda, colocamos en las ecuaciones anteriores A _r  = 1 (partícula entrante),A _l  =  r (reflexión), B _l  = 0 (ninguna partícula entrante de la derecha) y B _r  =  t (transmisión), y resolver para ry t aunque no tenemos ninguna ecuación en t . El resultado es

$${\ displaystyle t = {\ cfrac {1} {1 - {\ cfrac {m \ lambda} {i \ hbar ^ {2} k}}}} \, \!}

$${\ displaystyle r = {\ cfrac {1} {{\ cfrac {i \ hbar ^ {2} k} {m \ lambda}} - 1}} \, \!}

Debido a la simetría especular del modelo, las amplitudes de incidencia desde la derecha son las mismas que las de la izquierda. El resultado es que hay una probabilidad distinta de cero.

$${\ displaystyle R = | r | ^ {2} = {\ cfrac {1} {1 + {\ cfrac {\ hbar ^ {4} k ^ {2}} {m ^ {2} \ lambda ^ {2} }}}} = {\ cfrac {1} {1 + {\ cfrac {2 \ hbar ^ {2} E} {m \ lambda ^ {2}}}}}. \, \!}

Para que la partícula se refleje. Esto no depende del signo de λ , es decir, una barrera tiene la misma probabilidad de reflejar la partícula como un pozo. Esta es una diferencia significativa con respecto a la mecánica clásica, donde la probabilidad de reflexión sería 1 para la barrera (la partícula simplemente rebota) y 0 para el pozo (la partícula pasa a través del pozo sin ser perturbada).

En resumen, la probabilidad de transmisión es

$${\ displaystyle T = | t | ^ {2} = 1-R = {\ cfrac {1} {1 + {\ cfrac {m ^ {2} \ lambda ^ {2}} {\ hbar ^ {4} k ^ {2}}}}} = {\ cfrac {1} {1 + {\ cfrac {m \ lambda ^ {2}} {2 \ hbar ^ {2} E}}}} \, \!}.

Observaciones y aplicación [ editar ]

El cálculo presentado anteriormente puede parecer al principio poco realista y poco útil. Sin embargo, ha demostrado ser un modelo adecuado para una variedad de sistemas de la vida real.

Uno de estos ejemplos se refiere a las interfaces entre dos materiales conductores . En la mayor parte de los materiales, el movimiento de los electrones es casi libre y puede describirse mediante el término cinético en el hamiltoniano anterior con una masa m efectiva . A menudo, las superficies de tales materiales están cubiertas con capas de óxido o no son ideales por otras razones. Esta capa delgada y no conductora puede luego modelarse mediante un potencial de función delta local como el anterior. Los electrones pueden entonces hacer un túnel de un material a otro dando lugar a una corriente.

El funcionamiento de un microscopio de exploración de túneles (STM) se basa en este efecto de tunelización. En ese caso, la barrera se debe al aire entre la punta del STM y el objeto subyacente. La resistencia de la barrera se relaciona con que la separación es más fuerte cuanto más separados están los dos. Para un modelo más general de esta situación, vea Barrera de potencial finito (QM) . La barrera de potencial de función delta es el caso límite del modelo considerado allí para barreras muy altas y estrechas.

El modelo anterior es unidimensional, mientras que el espacio que nos rodea es tridimensional. Entonces, de hecho, uno debería resolver la ecuación de Schrödinger en tres dimensiones. Por otro lado, muchos sistemas solo cambian a lo largo de una dirección de coordenadas y son invariantes en la traducción a lo largo de los demás. La ecuación de Schrödinger puede entonces reducirse al caso considerado aquí por un Ansatz para la función de onda del tipo$${\ displaystyle \ Psi (x, y, z) = \ psi (x) \ phi (y, z) \, \!}.

Alternativamente, es posible generalizar la función delta para existir en la superficie de algún dominio D (ver Laplaciano del indicador ). ^[1]

El modelo de función delta es en realidad una versión unidimensional del átomo de hidrógeno de acuerdo con el método de escala dimensional desarrollado por el grupo de Dudley R. Herschbach ^[2] El modelo de función delta se vuelve particularmente útil con el modelo de función de Delta de Dirac de doble pozo que representa una versión unidimensional de la molécula de hidrógeno ion , como se muestra en la siguiente sección.

Doble potencial delta [ editar ]

Las funciones de onda simétrica y anti-simétrica para el modelo de función delta de Dirac de pozo doble con distancia "internuclear" R = 2.

La función delta de Dirac de pozo doble modela una molécula de hidrógeno diatómica mediante la ecuación de Schrödinger correspondiente:

$${\ displaystyle - {\ frac {\ hbar ^ {2}} {2m}} {\ frac {d ^ {2} \ psi} {dx ^ {2}}} (x) + V (x) \ psi ( x) = E \ psi (x)}

donde el potencial es ahora:

$${\ displaystyle V (x) = - q \ lambda \ left [\ delta \ left (x + {\ frac {R} {2}} \ right) + \ delta \ left (x - {\ frac {R} {2 }}\bien bien]}

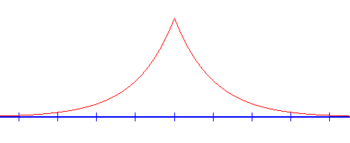
dónde {\ displaystyle 0 es la distancia "internuclear" con los picos de la función delta de Dirac (negativos) ubicados en x= ± R / 2 (se muestra en marrón en el diagrama). Teniendo en cuenta la relación de este modelo con su contraparte molecular tridimensional, usamos unidades atómicas y establecemos$${\ displaystyle \ hbar = m = 1}. aquí{\ displaystyle 0 <\ lambda <1 font="">Es un parámetro formalmente ajustable. Del caso del pozo único, podemos inferir el " ansatz " para que la solución sea:

$${\ displaystyle \ psi (x) ~ = ~ Ae ^ {- d \ left | x + {\ frac {R} {2}} \ right |} + Be ^ {- d \ left | x - {\ frac {R } {2}} \ right |}}

La coincidencia de la función de onda en los picos de la función delta de Dirac produce el determinante:

{\ displaystyle \ left | {\ begin {array} {cc} qd & qe ^ {- dR} \\ q \ lambda e ^ {- dR} & q \ lambda -d \ end {array}} \ right | = 0 \ quad {\ mbox {where}} \ quad E = - {\ frac {d ^ {2}} {2}} ~.}

Así, $${\ displaystyle d}Se encuentra gobernado por la ecuación pseudo-cuadrática :

$${\ displaystyle d _ {\ pm} (\ lambda) ~ = ~ {\ textstyle {\ frac {1} {2}}} q (\ lambda +1) \ pm {\ textstyle {\ frac {1} {2} }} \ left \ {q ^ {2} (1+ \ lambda) ^ {2} -4 \, \ lambda q ^ {2} \ lbrack 1-e ^ {- 2d _ {\ pm} (\ lambda) R }] \ right \} ^ {1/2}}

que tiene dos soluciones $${\ displaystyle d = d _ {\ pm}}. Para el caso de cargas iguales (caso homonuclear simétrico), λ = 1 y la pseudo-cuadrática se reduce a:

$${\ displaystyle d _ {\ pm} = q [1 \ pm e ^ {- d _ {\ pm} R}]}

El caso "+" corresponde a una función de onda simétrica sobre el punto medio (que se muestra en rojo en el diagrama) donde A = B y se llama gerade . Correspondientemente, el caso "-" es la función de onda que es anti-simétrica respecto del punto medio donde A = - B se llama ungerade (se muestra en verde en el diagrama). Representan una aproximación de los dos estados de energía discretos más bajos de los tridimensionales.$${\ displaystyle H_ {2} ^ {+}}y son útiles en su análisis. Las soluciones analíticas para los valores propios de energía para el caso de cargas simétricas están dadas por: ^[3]

$${\ displaystyle d _ {\ pm} = q ~ + ~ W (\ pm qRe ^ {- qR}) / R}

donde W es el estándar de la función W de Lambert . Tenga en cuenta que la energía más baja corresponde a la solución simétrica.$${\ displaystyle d _ {+}}. En el caso de cargas desiguales , y en este caso el problema molecular tridimensional, las soluciones vienen dadas por una generalización de la función de Lambert W (consulte la sección sobre generalización de la función de Lambert W y las referencias aquí).

Uno de los casos más interesantes es cuando qR ≤ 1, lo que resulta en$${\ displaystyle d _ {-} = 0}. Por lo tanto, uno tiene una solución de estado no trivial con E = 0. Para estos parámetros específicos, existen muchas propiedades interesantes, una de las cuales es el efecto inusual de que el coeficiente de transmisión es la unidad en energía cero.

matriz de densidad es una matriz que describe el estado estadístico de un sistema en mecánica cuántica . La matriz de densidad es especialmente útil para tratar estados mixtos , que consisten en un conjunto estadístico de varios sistemas cuánticos diferentes. Lo opuesto a un estado mixto es un estado puro . Los vectores de estado , también llamados kets , describen solo estados puros, mientras que una matriz de densidad puede describir tanto estados puros como mixtos.

La descripción de un estado cuántico por su matriz de densidad es un formalismo alternativo totalmente general a la descripción de un estado cuántico por su cet (vector de estado) o por su conjunto estadístico de kets. Sin embargo, en la práctica, a menudo es más conveniente usar matrices de densidad para cálculos que involucran estados mixtos, y usar kets para cálculos que involucren solo estados puros.

La matriz de densidad es el análogo mecánico-cuántico de una medida de probabilidad de fase-espacio (distribución de probabilidad de posición y momento) en la mecánica estadística clásica .

Los estados mixtos surgen en situaciones en las que el experimentador no sabe qué estados particulares están siendo manipulados. Los ejemplos incluyen un sistema en equilibrio térmico a una temperatura por encima del cero absoluto , o un sistema con un historial de preparación incierto o variable al azar (por lo que uno no sabe en qué estado se encuentra el sistema). Además, si un sistema cuántico tiene dos o más subsistemas que están enredados , entonces cada subsistema debe tratarse como un estado mixto, incluso si el sistema completo está en estado puro. ^[1] La matriz de densidad también es una herramienta crucial en la teoría de la decoherencia cuántica .

La matriz de densidad es una representación de un operador lineal llamado operador de densidad . La matriz de densidad se obtiene del operador de densidad mediante la elección de la base en el espacio subyacente. En la práctica, los términos matriz de densidad y operador de densidad a menudo se usan indistintamente. Tanto la matriz como el operador son autoadjuntos (o hermitianos ), semi-definidos positivos , de traza uno, y pueden ser de dimensión infinita .

Historia [ editar ]

El formalismo de los operadores de densidad y las matrices fue introducido por John von Neumann ^[3] en 1927 e independientemente, pero menos sistemáticamente por Lev Landau ^[4] [5] y Felix Bloch ^[6] en 1927 y 1946 respectivamente.

Estados puros y mixtos [ editar ]

En mecánica cuántica , el estado de un sistema cuántico está representado por un vector de estado , denotado$${\ displaystyle | \ psi \ rangle}(y pronunciado ket ). Un sistema cuántico con un vector de estado.$${\ displaystyle | \ psi \ rangle}Se llama un estado puro . Sin embargo, también es posible que un sistema esté en un conjunto estadístico de diferentes vectores de estado: por ejemplo, puede haber un 50% de probabilidad de que el vector de estado sea$${\ displaystyle | \ psi _ {1} \ rangle} y un 50% de probabilidad de que el vector de estado sea $${\ displaystyle | \ psi _ {2} \ rangle}. Este sistema estaría en un estado mixto . La matriz de densidad es especialmente útil para estados mixtos, porque cualquier estado, puro o mixto, se puede caracterizar por una matriz de densidad única. ^{[ cita requerida ]}

Un estado mixto es diferente de una superposición cuántica . Las probabilidades en un estado mixto son probabilidades clásicas (como en las probabilidades que uno aprende en la teoría / estadística de probabilidad clásica), a diferencia de las probabilidades cuánticas en una superposición cuántica. De hecho, una superposición cuántica de estados puros es otro estado puro, por ejemplo$${\ displaystyle | \ psi \ rangle = (| \ psi _ {1} \ rangle + | \ psi _ {2} \ rangle) / {\ sqrt {2}}}. En este caso, los coeficientes.$${\ displaystyle 1 / {\ sqrt {2}}}No son probabilidades, sino amplitudes de probabilidad . ^{[ cita requerida ]}

Ejemplo: polarización de la luz [ editar ]

La bombilla incandescente (1) emite fotones polarizados completamente aleatorios (2) con matriz de densidad de estado mixto
{\ displaystyle {\ begin {bmatrix} 0.5 & 0 \\ 0 & 0.5 \\\ end {bmatrix}}} 。
Después de pasar por el polarizador de plano vertical (3), los fotones restantes están todos polarizados verticalmente (4) y tienen una matriz de densidad de estado puro
{\ displaystyle {\ begin {bmatrix} 1 & 0 \\ 0 & 0 \\\ end {bmatrix}}} 。

Un ejemplo de estados puros y mixtos es la polarización de la luz . Los fotones pueden tener dos helicities , correspondientes a dos estados cuánticos ortogonales,$${\ displaystyle | R \ rangle}( polarización circular derecha ) y$${\ displaystyle | L \ rangle}( polarización circular izquierda ). Un fotón también puede estar en un estado de superposición, como$${\ displaystyle (| R \ rangle + | L \ rangle) / {\ sqrt {2}}} (polarización vertical) o $${\ displaystyle (| R \ rangle - | L \ rangle) / {\ sqrt {2}}}(polarización horizontal). Más generalmente, puede ser en cualquier estado$${\ displaystyle \ alpha | R \ rangle + \ beta | L \ rangle} (con $${\ displaystyle | \ alpha | ^ {2} + | \ beta | ^ {2} = 1}), correspondiente a la polarización lineal , circular o elíptica . Si pasamos$${\ displaystyle (| R \ rangle + | L \ rangle) / {\ sqrt {2}}}luz polarizada a través de un polarizador circular que permite ya sea solo$${\ displaystyle | R \ rangle}luz polarizada, o solo $${\ displaystyle | L \ rangle}En la luz polarizada, la intensidad se reduciría a la mitad en ambos casos. Esto puede hacer que parezca que la mitad de los fotones están en estado.$${\ displaystyle | R \ rangle} y la otra mitad en estado $${\ displaystyle | L \ rangle}. Pero esto no es correcto: ambos$${\ displaystyle | R \ rangle} y $${\ displaystyle | L \ rangle}los fotones son parcialmente absorbidos por un polarizador lineal vertical , pero el$${\ displaystyle (| R \ rangle + | L \ rangle) / {\ sqrt {2}}}la luz pasará a través de ese polarizador sin absorción alguna. ^{[ cita requerida ]}

Sin embargo, la luz no polarizada (como la luz de una bombilla incandescente ) es diferente de cualquier estado como$${\ displaystyle \ alpha | R \ rangle + \ beta | L \ rangle}(polarización lineal, circular, o elíptica). A diferencia de la luz polarizada lineal o elípticamente, pasa a través de un polarizador con una pérdida de intensidad del 50%, independientemente de la orientación del polarizador; y, a diferencia de la luz polarizada circularmente, no se puede polarizar linealmente con ninguna placa de ondaporque la polarización orientada al azar surgirá de una placa de onda con orientación aleatoria. De hecho, la luz no polarizada no se puede describir como ningún estado de la forma$${\ displaystyle \ alpha | R \ rangle + \ beta | L \ rangle}en un sentido definido Sin embargo, la luz no polarizada se puede describir con promedios de conjunto, por ejemplo, que cada fotón es$${\ displaystyle | R \ rangle}con 50% de probabilidad o $${\ displaystyle | L \ rangle}con 50% de probabilidad. El mismo comportamiento ocurriría si cada fotón estuviera polarizado verticalmente con una probabilidad del 50% o polarizado horizontalmente con una probabilidad del 50%. ^{[ cita requerida ]}

Por lo tanto, la luz no polarizada no se puede describir con ningún estado puro, pero se puede describir como un conjunto estadístico de estados puros en al menos dos formas (el conjunto de la mitad izquierda y la mitad derecha circularmente polarizadas, o el conjunto de la mitad verticalmente y la mitad horizontalmente lineal polarizado). Estos dos conjuntos son completamente indistinguibles experimentalmente, y por lo tanto se consideran el mismo estado mixto. Una de las ventajas de la matriz de densidad es que solo hay una matriz de densidad para cada estado mixto, mientras que hay muchos conjuntos estadísticos de estados puros para cada estado mixto. Sin embargo, la matriz de densidad contiene toda la información necesaria para calcular cualquier propiedad medible del estado mixto. ^{[ cita requerida ]}

¿De dónde vienen los estados mixtos? Para responder eso, considera cómo generar luz no polarizada. Una forma es usar un sistema en equilibrio térmico , una mezcla estadística de enormes cantidades de microestados , cada uno con una cierta probabilidad (el factor de Boltzmann ), que cambia rápidamente de uno a otro debido a las fluctuaciones térmicas . La aleatoriedad térmica explica por qué una bombilla incandescente , por ejemplo, emite luz no polarizada. Una segunda forma de generar luz no polarizada es introducir incertidumbre en la preparación del sistema, por ejemplo, pasarlo a través de un cristal birrefringente.con una superficie rugosa, de modo que partes ligeramente diferentes del haz adquieren polarizaciones diferentes. Una tercera forma de generar luz no polarizada utiliza una configuración de EPR : una descomposición radioactiva puede emitir dos fotones que viajan en direcciones opuestas, en el estado cuántico$${\ displaystyle (| R, L \ rangle + | L, R \ rangle) / {\ sqrt {2}}}. Los dos fotones juntos están en un estado puro, pero si solo miras a uno de los fotones e ignoras al otro, el fotón se comporta como una luz no polarizada. ^{[ cita requerida ]}

Más generalmente, los estados mixtos surgen comúnmente de una mezcla estadística del estado de inicio (como en el equilibrio térmico), de la incertidumbre en el procedimiento de preparación (como los caminos ligeramente diferentes que puede recorrer un fotón), o de mirar un subsistema enredado con algo más. ^{[ cita requerida ]}

Definición [ editar ]

Para un espacio de función de dimensión finita, el operador de densidad más general tiene la forma

$${\ displaystyle \ rho = \ sum _ {j} p_ {j} | \ psi _ {j} \ rangle \ langle \ psi _ {j} |}

donde los coeficientes p _j no son negativos y suman uno, y$${\ displaystyle \ textstyle | \ psi _ {j} \ rangle \ langle \ psi _ {j} |}Es un producto exterior escrito en notación bra-ket . Esto representa un estado mixto, con probabilidad p _{j de} que el sistema está en estado puro$${\ displaystyle \ textstyle | \ psi _ {j} \ rangle}. ^{[ cita requerida ]}

Para el ejemplo anterior de luz no polarizada, el operador de densidad es

$${\ displaystyle \ rho = {\ tfrac {1} {2}} | R \ rangle \ langle R | + {\ tfrac {1} {2}} | L \ rangle \ langle L |.}

dónde $${\ displaystyle \ textstyle | L \ rangle} es el estado del fotón polarizado circularmente a la izquierda y $${\ displaystyle \ textstyle | R \ rangle}Es el estado del fotón polarizado circularmente hacia la derecha. ^{[ cita requerida ]}

Diferentes conjuntos estadísticos con la misma matriz de densidad [ editar ]

Una sección anterior dio un ejemplo de dos conjuntos estadísticos de estados puros que tienen el mismo operador de densidad: la luz no polarizada se puede describir como 50% polarizada circular derecha y 50% polarizada circular izquierda, o 50% polarizada horizontalmente y 50% polarizado verticalmente. Tales conjuntos o mezclas equivalentes no pueden distinguirse por ninguna medida. Esta equivalencia se puede caracterizar con precisión. Dos conjuntos, ψ 'definen el mismo operador de densidad si y solo si hay un operador Unitario U con

$${\ displaystyle | \ psi _ {i} '\ rangle {\ sqrt {p_ {i}'}} = \ sum _ {j} u_ {ij} | \ psi _ {j} \ rangle {\ sqrt {p_ { j}}} ~.}

Esto es simplemente una reafirmación del siguiente hecho del álgebra lineal: para dos matrices cuadradas M y N, MM ^* = NN ^* si y solo si M = NU para alguna U unitaria . (Consulte la raíz cuadrada de una matriz para obtener más detalles). Por lo tanto, existe una libertad unitaria en la mezcla de cet o conjunto que proporciona el mismo operador de densidad. Sin embargo, si los kets que componen la mezcla están restringidos a una base ortonormal específica , entonces las probabilidades p _j originales son recuperables únicamente de esa base, como los valores propios de la matriz de densidad. ^{Elcita requerida ]}

Propiedades matemáticas y condición de pureza [ editar ]

En el lenguaje del operador, un operador de densidad es un semidefinida positiva , hermitiana operador del rastro 1 que actúa sobre el espacio de estados. ^[1] Un operador de densidad describe un estado puro si es una proyección de rango uno. De manera equivalente, un operador de densidad ρ describe un estado puro si y solo si

$${\ displaystyle \ rho = \ rho ^ {2}},

Es decir, el estado es idempotente . Esto es cierto independientemente de si H es de dimensión finita o no. ^{[ cita requerida ]}

Geométricamente, cuando el estado no es expresable como una combinación convexa de otros estados, es un estado puro. ^[1] La familia de estados mixtos es un conjunto convexo y un estado es puro si es un punto extremode ese conjunto.

Del teorema espectral de los operadores autoadjuntos compactos se desprende que cada estado mixto es una combinación convexa contable de estados puros. Esta representación no es única. Además, un teorema de Andrew Gleason establece que ciertas funciones definidas en la familia de proyecciones y tomando valores en [0,1] (que pueden considerarse como análogos cuánticos de medidas de probabilidad) están determinadas por estados mixtos únicos. Ver la lógica cuántica para más detalles. ^{[ cita requerida ]}

Medición [ editar ]

Sea A un observable del sistema, y ​​supongamos que el conjunto está en un estado mixto tal que cada uno de los estados puros$${\ displaystyle \ textstyle | \ psi _ {j} \ rangle}Ocurre con probabilidad p _j . Entonces el operador de densidad correspondiente es:

$${\ displaystyle \ rho = \ sum _ {j} p_ {j} | \ psi _ {j} \ rangle \ langle \ psi _ {j} |.}

El valor de expectativa de la medición se puede calcular extendiendo desde el caso de estados puros (ver Medición en mecánica cuántica ):

$${\ displaystyle \ langle A \ rangle = \ sum _ {j} p_ {j} \ langle \ psi _ {j} | A | \ psi _ {j} \ rangle = \ sum _ {j} p_ {j} \ operatorname {tr} \ left (| \ psi _ {j} \ rangle \ langle \ psi _ {j} | A \ right) = \ sum _ {j} \ operatorname {tr} \ left (p_ {j} | \ psi _ {j} \ rangle \ langle \ psi _ {j} | A \ right) = \ operatorname {tr} \ left (\ sum _ {j} p_ {j} | \ psi _ {j} \ rangle \ langle \ psi _ {j} | A \ right) = \ operatorname {tr} (\ rho A),}

dónde $${\ displaystyle \ operatorname {tr}}denota traza . Así, la expresión familiar.$${\ displaystyle \ langle A \ rangle = \ langle \ psi | A | \ psi \ rangle} por estados puros es reemplazado por

$${\ displaystyle \ langle A \ rangle = \ operatorname {tr} (\ rho A)}

para estados mixtos.

Además, si A tiene resolución espectral.

$${\ displaystyle A = \ sum _ {i} a_ {i} | a_ {i} \ rangle \ langle a_ {i} | = \ sum _ {i} a_ {i} P_ {i},}

dónde $${\ displaystyle P_ {i} = | a_ {i} \ rangle \ langle a_ {i} |}, el operador de densidad correspondiente después de la medición viene dado por:

$${\ displaystyle \; \ rho '= \ sum _ {i} P_ {i} \ rho P_ {i}.}

Tenga en cuenta que el operador de densidad anterior describe el conjunto completo después de la medición. El subconjunto para el cual el resultado de la medición fue el valor particular a _i lo describe el operador de densidad diferente

$${\ displaystyle \ rho _ {i} '= {\ frac {P_ {i} \ rho P_ {i}} {\ operatorname {tr} [\ rho P_ {i}]}}.}

Esto es cierto asumiendo que $${\ displaystyle \ textstyle | a_ {i} \ rangle}es el único eigenket (hasta la fase ) con un valor propio a _i ; más generalmente, P _i en esta expresión sería reemplazado por el operador de proyección en el espacio propiocorrespondiente al valor propio a _i .

Más en general, supongamos $${\ displaystyle \ Phi}es una función que asocia a cada observable A un número$${\ displaystyle \ Phi (A)}, Que podemos considerar como el "valor esperado" de un . Si$${\ displaystyle \ Phi} satisface algunas propiedades naturales (como dar valores positivos en operadores positivos), entonces hay una matriz de densidad única $${\ displaystyle \ rho} tal que

$${\ displaystyle \ Phi (A) = \ operatorname {tr} (\ rho A)}

para todos A . ^[1] Es decir, cualquier "familia de valores de expectativa" razonable es representable por una matriz de densidad. Esta observación sugiere que las matrices de densidad son la noción más general de un estado cuántico.

Entropía [ editar ]

La entropía de von Neumann $${\ displaystyle S} de una mezcla puede expresarse en términos de valores propios de $${\ displaystyle \ rho}o en términos de la traza y el logaritmo del operador de densidad$${\ displaystyle \ rho}. Ya que$${\ displaystyle \ rho}es un operador semi-definido positivo, tiene una descomposición espectral tal que$${\ displaystyle \ rho = \ textstyle \ sum _ {i} \ lambda _ {i} | \ varphi _ {i} \ rangle \ langle \ varphi _ {i} |}, dónde $${\ displaystyle | \ varphi _ {i} \ rangle} son vectores ortonormales, {\ displaystyle \ lambda _ {i}> 0}y $${\ displaystyle \ textstyle \ sum \ lambda _ {i} = 1}. Luego la entropía de un sistema cuántico con matriz de densidad.$${\ displaystyle \ rho} es

$${\ displaystyle S = - \ sum _ {i} \ lambda _ {i} \ ln \ lambda _ {i} = - \ operatorname {tr} (\ rho \ ln \ rho).}

Esta entropía puede aumentar, pero nunca disminuir, con una medida proyectiva. Sin embargo, las mediciones generalizadas pueden disminuir la entropía. ^[7] [8] La entropía de un estado puro es cero, mientras que la de una mezcla adecuada siempre es mayor que cero. Por lo tanto, un estado puro se puede convertir en una mezcla mediante una medición, pero una mezcla adecuada nunca se puede convertir en un estado puro. Así, el acto de medición induce un cambio fundamental irreversible en la matriz de densidad; esto es análogo al "colapso" del vector de estado, o al colapso de la función de onda . Quizás contraintuitivamente, la medición en realidad disminuye la información al borrar la interferencia cuántica en el sistema compuesto, verEl entrelazamiento cuántico , la selección y la decoherencia cuántica .

Un subsistema de un sistema más grande puede pasar de un estado mixto a uno puro, pero solo aumentando la entropía de von Neumann en otras partes del sistema. Esto es análogo a cómo se puede bajar la entropía de un objeto poniéndolo en un refrigerador: el aire que se encuentra fuera del intercambiador de calor del refrigerador se calienta, ganando aún más entropía de la que perdió el objeto en el refrigerador. Ver segunda ley de la termodinámica . Ver Entropía en termodinámica y teoría de la información .

Sistemas y subsistemas [ editar ]

Otra motivación para considerar matrices de densidad proviene de la consideración de los sistemas y sus subsistemas. Supongamos que tenemos dos sistemas cuánticos, descritos por los espacios de Hilbert.$${\ displaystyle {\ mathcal {H}} _ {1}} y $${\ displaystyle {\ mathcal {H}} _ {2}}. El sistema compuesto es entonces el producto tensorial. $${\ displaystyle {\ mathcal {H}} _ {1} \ otimes {\ mathcal {H}} _ {2}}De los dos espacios de Hilbert. Supongamos ahora que el sistema compuesto está en estado puro$${\ displaystyle \ psi \ en {\ mathcal {H}} _ {1} \ otimes {\ mathcal {H}} _ {2}}. Si$${\ displaystyle \ psi} sucede tener la forma especial $${\ displaystyle \ psi = \ psi _ {1} \ otimes \ psi _ {2}}, entonces podemos decir razonablemente que el estado del primer subsistema es $${\ displaystyle \ psi _ {1}}. En este caso, decimos que los dos sistemas no están enredados. En general, sin embargo,$${\ displaystyle \ psi} no se descompondrá como un único producto tensorial de vectores en $${\ displaystyle {\ mathcal {H}} _ {1}} y $${\ displaystyle {\ mathcal {H}} _ {2}}. Si$${\ displaystyle \ psi}no se puede descomponer como un solo tensor producto de estados en los sistemas de componentes, decimos que los dos sistemas están enredados. En ese caso, no hay una manera razonable de asociar un estado puro$${\ displaystyle \ psi _ {1} \ in {\ mathcal {H}} _ {1}} al Estado $${\ displaystyle \ psi \ en {\ mathcal {H}} _ {1} \ otimes {\ mathcal {H}} _ {2}}. ^[1]

Si, por ejemplo, tenemos una función de onda. $${\ displaystyle \ psi (x_ {1}, x_ {2})} Al describir el estado de dos partículas, no hay una forma natural de construir una función de onda (es decir, estado puro) $${\ displaystyle \ psi _ {1} (x_ {1})} que describe los estados de la primera partícula, a menos que $${\ displaystyle \ psi (x_ {1}, x_ {2})} pasa a ser un producto de una función $${\ displaystyle \ psi _ {1} (x_ {1})} y una función $${\ displaystyle \ psi _ {2} (x_ {2})}.

El resultado de la discusión anterior es que incluso si el sistema total está en estado puro, los diversos subsistemas que lo componen estarán típicamente en estados mixtos. Por lo tanto, el uso de matrices de densidad es inevitable.

Por otro lado, ya sea que el sistema compuesto esté en estado puro o mixto, podemos construir perfectamente una matriz de densidad que describa el estado de $${\ displaystyle {\ mathcal {H}} _ {1}}. Denota la matriz de densidad del sistema compuesto de dos sistemas por$${\ displaystyle \ rho}. Entonces el estado de, digamos,$${\ displaystyle {\ mathcal {H}} _ {1}}, se describe por un operador de densidad reducida , dado por tomar el "trazado parcial" de$${\ displaystyle \ rho} terminado $${\ displaystyle {\ mathcal {H}} _ {2}}. ^[1]

Si el estado de $${\ displaystyle {\ mathcal {H}} _ {1} \ otimes {\ mathcal {H}} _ {2}} Resulta ser una matriz de densidad de la forma especial. $${\ displaystyle \ rho = \ rho _ {1} \ otimes \ rho _ {2}} dónde $${\ displaystyle \ rho _ {1}} y $${\ displaystyle \ rho _ {2}}son matrices de densidad en $${\ displaystyle {\ mathcal {H}} _ {1}} y $${\ displaystyle {\ mathcal {H}} _ {2}}, luego la traza parcial de $${\ displaystyle \ rho} con respecto a $${\ displaystyle {\ mathcal {H}} _ {2}} es solo $${\ displaystyle \ rho _ {1}}. Un tipico$${\ displaystyle \ rho} Sin embargo, no será de esta forma.

La ecuación de von Neumann para la evolución del tiempo [ editar ]

Ver también: Teorema de Liouville (Hamiltoniano) § Ecuación cuántica de Liouville

Así como la ecuación de Schrödinger describe cómo evolucionan los estados puros en el tiempo, la ecuación de von Neumann (también conocida como la ecuación de Liouville-von Neumann ) describe cómo un operador de densidad evoluciona en el tiempo (de hecho, las dos ecuaciones son equivalentes, en el sentido de que cualquiera puede derivarse de la otra.) La ecuación de von Neumann dicta que ^[9] [10]

$${\ displaystyle i \ hbar {\ frac {\ partial \ rho} {\ partial t}} = [H, \ rho] ~,}

donde los paréntesis denotan un conmutador .

Tenga en cuenta que esta ecuación solo se mantiene cuando se considera que el operador de densidad está en la imagen de Schrödinger , aunque a primera vista parece que esta ecuación emula la ecuación de movimiento de Heisenberg en la imagen de Heisenberg , con una diferencia de signo crucial:

$${\ displaystyle i \ hbar {\ frac {dA ^ {(H)}} {dt}} = - [H, A ^ {(H)}] ~,}

dónde $${\ displaystyle A ^ {(H)} (t)}es un operador de imagen de Heisenberg ; pero en esta imagen, la matriz de densidad no depende del tiempo , y el signo relativo garantiza que la derivada del tiempo del valor esperado$${\ displaystyle \ langle A \ rangle}sale lo mismo que en la imagen de Schrödinger . ^[1]

Hacer que el operador de densidad esté en la imagen de Schrödinger tiene sentido, ya que está compuesto de kets y sujetadores 'Schrödinger' que evolucionaron en el tiempo, según la imagen de Schrödinger. Si el Hamiltoniano es independiente del tiempo, esta ecuación diferencial se puede resolver fácilmente para obtener

$${\ displaystyle \ rho (t) = e ^ {- iHt / \ hbar} \ rho (0) e ^ {iHt / \ hbar}.}

Para un hamiltoniano más general, si $${\ displaystyle G (t)} es el propagador de la función de onda en algún intervalo, entonces la evolución temporal de la matriz de densidad en ese mismo intervalo viene dada por

$${\ displaystyle \ rho (t) = G (t) \ rho (0) G (t) ^ {\ dagger}.}

Sin embargo, ^[11] la matriz de densidad contiene probabilidades tanto clásicas como mecánicas cuánticas, es necesario tener en cuenta los cambios en ambos en presencia de influencias externas.

"Quantum Liouville", ecuación de Moyal [ editar ]

El operador de matriz de densidad también se puede realizar en el espacio de fase . Bajo el mapa de Wigner , la matriz de densidad se transforma en la función de Wigner equivalente ,

$${\ displaystyle W (x, p) {\ stackrel {\ mathrm {def}} {=}} {\ frac {1} {\ pi \ hbar}} \ int _ {- \ infty} ^ {\ infty} \ psi ^ {*} (x + y) \ psi (xy) e ^ {2ipy / \ hbar} \, dy.}

La ecuación para la evolución temporal de la función de Wigner es entonces la transformada de Wigner de la ecuación de von Neumann anterior,

$${\ displaystyle {\ frac {\ parcial W (q, p, t)} {\ parcial t}} = - \ {\ {W (q, p, t), H (q, p) \} \}, }

donde H ( q , p ) es el Hamiltoniano, y {{•, •}} es el corchete Moyal , la transformada del conmutador cuántico .

La ecuación de evolución para la función de Wigner es entonces análoga a la de su límite clásico, la ecuación de Liouville de la física clásica . En el límite de la desaparición de la constante de Planck ħ , W ( q , p , t ) se reduce a la función de densidad de probabilidad clásica de Liouville en el espacio de fase .

La ecuación de Liouville clásica se puede resolver utilizando el método de características para ecuaciones diferenciales parciales, siendo las ecuaciones características las ecuaciones de Hamilton . La ecuación de Moyal en mecánica cuántica admite de manera similar soluciones formales en términos de características cuánticas , basadas en el ∗ −producto del espacio de fase, aunque, en la práctica real, la búsqueda de soluciones sigue métodos diferentes.

Aplicaciones de ejemplo [ editar ]

Las matrices de densidad son una herramienta básica de la mecánica cuántica, y aparecen al menos ocasionalmente en casi cualquier tipo de cálculo cuántico-mecánico. Algunos ejemplos específicos donde las matrices de densidad son especialmente útiles y comunes son los siguientes:

• La teoría de la decoherencia cuántica típicamente involucra sistemas cuánticos no aislados que desarrollan el enredo con otros sistemas, incluyendo aparatos de medición. Las matrices de densidad hacen que sea mucho más fácil describir el proceso y calcular sus consecuencias.
• De manera similar, en la computación cuántica , la teoría de la información cuántica y otros campos donde la preparación del estado es ruidosa y puede ocurrir una decoherencia, las matrices de densidad se usan con frecuencia.
  • La tomografía cuántica es el proceso de medir experimentalmente la matriz de densidad de un sistema ^[12].
• Cuando se analiza un sistema con muchos electrones, como un átomo o una molécula , una primera aproximación imperfecta pero útil es tratar los electrones como no correlacionados o cada uno de ellos con una función de onda de partícula única independiente. Este es el punto de partida habitual cuando se construye el determinante de Slater en el método de Hartree-Fock . Si hay N electrones que llenan las Nfunciones de onda de una sola partícula$${\ displaystyle | \ psi _ {i} \ rangle}, entonces la colección de N electrones juntos se puede caracterizar por una matriz de densidad$${\ displaystyle \ sum _ {i = 1} ^ {N} | \ psi _ {i} \ rangle \ langle \ psi _ {i} |}.

C * -formación algebraica de estados [ editar ]

Ahora se acepta en general que la descripción de la mecánica cuántica en la que todos los operadores autoadjuntos representan observables es insostenible. ^[13] [14] Por esta razón, observables se identifican con los elementos de un extracto C * -algebra A (que es uno sin una representación distingue como un álgebra de operadores) y estados son positivos funcionales lineales en A . Sin embargo, al utilizar la construcción GNS , podemos recuperar espacios de Hilbert que realizan A como una subalgebra de operadores.

Geométricamente, un estado puro en un C * álgebra A es un estado que es un punto extremo del conjunto de todos los estados en una . Por propiedades de la construcción GNS estos estados corresponden a representaciones irreducibles de A .

Los estados del álgebra C * de los operadores compactos K ( H ) corresponden exactamente a los operadores de densidad, y por lo tanto los estados puros de K ( H ) son exactamente los estados puros en el sentido de la mecánica cuántica.

Se puede ver que la formulación algebraica C * incluye sistemas tanto clásicos como cuánticos. Cuando el sistema es clásico, el álgebra de observables se convierte en una álgebra C * abeliana. En ese caso, los estados se convierten en medidas de probabilidad, como se señala en la introducción.