MECÁNICA CUÁNTICA

 reglas de correspondencia rigen el principio de reemplazar cantidades físicas con operadores .

Dichos reemplazos incluyen energía y momento, que pueden derivarse informalmente de la obtención de las derivaciones de tiempo y espacio de la función de onda plana . Estos muestran una similitud con el principio de incertidumbre heisenberg .

Ejemplos de reglas de correspondencia incluyen:

Cantidad	Operador
Energía ( hamiltoniano )	$${\ displaystyle i \ hbar {\ frac {\ partial} {\ partial t}}}
Impulso	$${\ displaystyle -i \ hbar \ nabla}

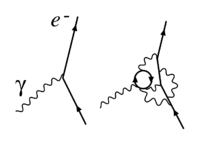
parámetro de acoplamiento constante o calibre de acoplamiento (o, más simplemente, un acoplamiento ), es un número que determina la fuerza de la fuerza ejercida en una interacción . Por lo general, el Lagrangiano o el Hamiltoniano de un sistema que describe una interacción se puede separar en una parte cinética y una parte de interacción . La constante de acoplamiento determina la fuerza de la parte de interacción con respecto a la parte cinética, o entre dos sectores de la parte de interacción. Por ejemplo, la carga eléctrica.de una partícula es una constante de acoplamiento que caracteriza una interacción con dos campos de carga y un campo de fotones (de ahí el diagrama de Feynman común con dos flechas y una línea ondulada). Dado que los fotones llevan el electromagnetismo , este acoplamiento determina la fuerza con que los electrones sienten esa fuerza, y su valor queda fijado por el experimento.

Un acoplamiento juega un papel importante en la dinámica. Por ejemplo, a menudo se establecen jerarquías de aproximación basadas en la importancia de varias constantes de acoplamiento. En el movimiento de un gran trozo de hierro magnetizado, las fuerzas magnéticas pueden ser más importantes que las fuerzas gravitacionales debido a las magnitudes relativas de las constantes de acoplamiento. Sin embargo, en la mecánica clásica , generalmente se toman estas decisiones directamente al comparar fuerzas.

Feynman diagram

Constante de estructura fina [ editar ]

Los acoplamientos surgen naturalmente en una teoría cuántica de campos . Se juega un papel especial en las teorías cuánticas relativistas mediante acoplamientos que son adimensionales ; Es decir, son números puros. Un ejemplo de una constante sin dimensiones es la constante de estructura fina ,

$${\ displaystyle \ alpha = {\ frac {e ^ {2}} {4 \ pi \ varepsilon _ {0} \ hbar c}},}

donde e es la carga de un electrón ,$${\ displaystyle \ varepsilon _ {0}}es la permitividad del espacio libre , ℏ es la constante de Planck reducida y c es la velocidad de la luz . Esta constante es proporcional al cuadrado de la fuerza de acoplamiento de la carga de un electrón al campo electromagnético .

Acoplamiento de calibre [ editar ]

En una teoría del calibre no abeliano , el parámetro de acoplamiento del calibre , g , aparece en el Lagrangiano como

$${\ displaystyle {\ frac {1} {4g ^ {2}}} {\ rm {Tr}} \, G _ {\ mu \ nu} G ^ {\ mu \ nu},}

(donde G es el tensor de campo del indicador ) en algunas convenciones. En otra convención ampliamente utilizada, G se vuelve a escalar para que el coeficiente del término cinético sea 1/4 y$${\ displaystyle g}Aparece en el derivado covariante . Esto debe entenderse como similar a una versión adimensional de la carga elemental definida como

$${\ displaystyle {\ frac {e} {\ sqrt {\ varepsilon _ {0} \ hbar c}}} = {\ sqrt {4 \ pi \ alpha}} \ approx 0.30282212 \ ~~.}

Acoplamiento débil y fuerte [ editar ]

En una teoría cuántica de campos con un acoplamiento ad dimensional g , si g es mucho menor que 1, se dice que la teoría está débilmente acoplada . En este caso, está bien descrito por una expansión en los poderes de g , llamada teoría de perturbación . Si la constante de acoplamiento es de orden uno o mayor, se dice que la teoría está fuertemente acoplada . Un ejemplo de esto último es la teoría hadrónica de las interacciones fuertes (por lo que se denomina fuerte en primer lugar). En tal caso, se deben utilizar métodos no perturbativos para investigar la teoría.

Correr acoplamiento [ editar ]

Se puede probar una teoría de campo cuántico en tiempos o distancias cortas cambiando la longitud de onda o el momento, k , de la sonda utilizada. Con una sonda de alta frecuencia (es decir, tiempo corto), se ven partículas virtuales que participan en cada proceso. Esta aparente violación de la conservación de la energía puede entenderse heurísticamente al examinar la relación de incertidumbre.

$${\ displaystyle \ Delta E \ Delta t \ geq {\ frac {\ hbar} {2}},}

que virtualmente permite tales violaciones en tiempos cortos.

El comentario anterior solo se aplica a algunas formulaciones de la teoría cuántica de campos, en particular, la cuantificación canónica en la imagen de interacción . En otras formulaciones, el mismo evento es descrito por partículas "virtuales" que salen de la cubierta de masa . Tales procesos renormalizan el acoplamiento y lo hacen dependiente de la escala de energía, μ , en la cual uno observa el acoplamiento. La dependencia de un acoplamiento g (μ) en la escala de energía se conoce como "funcionamiento del acoplamiento". La teoría del funcionamiento de los acoplamientos está dada por el grupo de renormalización., aunque debe tenerse en cuenta que el grupo de renormalización es un concepto más general que describe cualquier tipo de invariancia de escala en un sistema físico (consulte el artículo completo para obtener más información).

Funciones beta [ editar ]

Artículo principal: Función Beta (física).

En la teoría cuántica de campos, una función beta, β ( g ), codifica la ejecución de un parámetro de acoplamiento, g . Se define por la relación.

$${\ displaystyle \ beta (g) = \ mu {\ frac {\ partial g} {\ partial \ mu}} = {\ frac {\ partial g} {\ partial \ ln \ mu}},}

donde μ es la escala de energía del proceso físico dado. Si las funciones beta de una teoría cuántica de campos desaparecen, entonces la teoría es invariante de escala .

Los parámetros de acoplamiento de una teoría de campo cuántica pueden fluir incluso si la teoría de campoclásica correspondiente es invariante en escala . En este caso, la función beta distinta de cero nos dice que la invariancia de escala clásica es anómala .

QED y el polo de Landau [ editar ]

Si una función beta es positiva, el acoplamiento correspondiente aumenta al aumentar la energía. Un ejemplo es la electrodinámica cuántica (QED, por sus siglas en inglés), donde, mediante la teoría de la perturbación, se encuentra que la función beta es positiva. En particular, a bajas energías, α ≈ 1/137 , mientras que en la escala del bosón Z , aproximadamente 90  GeV , se mide α ≈ 1/127 .

Además, la función beta perturbativa nos dice que el acoplamiento continúa aumentando, y el QED se acopla fuertemente a alta energía. De hecho, el acoplamiento aparentemente se vuelve infinito en alguna energía finita. Este fenómeno fue observado por primera vez por Lev Landau , y se llama el polo de Landau . Sin embargo, no se puede esperar que la función beta perturbativa proporcione resultados precisos en un fuerte acoplamiento, por lo que es probable que el polo de Landau sea un artefacto de aplicar la teoría de la perturbación en una situación en la que ya no sea válida. El verdadero comportamiento de escalado de$${\ displaystyle \ alpha} En general, las energías no se conocen.

QCD y la libertad asintótica [ editar ]

En las teorías de gauge no abelianas, la función beta puede ser negativa, como lo encontraron por primera vez Frank Wilczek , David Politzer y David Gross . Un ejemplo de esto es la función beta para la cromodinámica cuántica (QCD), y como resultado, el acoplamiento QCD disminuye a altas energías.

Además, el acoplamiento disminuye logarítmicamente, un fenómeno conocido como libertad asintótica (cuyo descubrimiento fue galardonado con el Premio Nobel de Física en 2004). El acoplamiento disminuye aproximadamente a medida que

$${\ displaystyle \ alpha _ {\ text {s}} (k ^ {2}) \ {\ stackrel {\ mathrm {def}} {=}} \ {\ frac {g _ {\ text {s}} ^ { 2} (k ^ {2})} {4 \ pi}} \ approx {\ frac {1} {\ beta _ {0} \ ln \ left ({\ frac {k ^ {2}} {\ Lambda ^ {2}}} \ derecha)}},}

donde β ₀ es una constante calculada primero por Wilczek, Gross y Politzer.

Por el contrario, el acoplamiento aumenta con la energía decreciente. Esto significa que el acoplamiento se hace grande a bajas energías, y uno ya no puede confiar en la teoría de la perturbación .

Escala QCD [ editar ]

En la cromodinámica cuántica (QCD), la cantidad se denomina escala QCD . El valor es

$${\ displaystyle \ Lambda _ {MS} = 218 \ pm 24 {\ text {MeV}}.}

Este valor se debe utilizar en una escala por encima de la masa del quark inferior de aproximadamente 5  GeV . El significado de Λ _MS se da en el artículo sobre la transmutación dimensional .

La relación de masa protón a electrón está determinada principalmente por la escala QCD.

La teoría de cuerdas [ editar ]

Existe una situación notablemente diferente en la teoría de cuerdas, ya que incluye un dilaton . Un análisis del espectro de cadenas muestra que este campo debe estar presente, ya sea en la cadena bosónica o en el sector NS-NS de la supercuerdas . Usando operadores de vértices , se puede ver que emocionante este campo es equivalente a agregar un término a la acción donde un campo escalar se acopla al escalar de Ricci. Este campo es, por lo tanto, una función completa digna de acoplar constantes. Estas constantes de acoplamiento no son parámetros predeterminados, ajustables o universales; dependen del espacio y el tiempo de una manera que se determina dinámicamente. Las fuentes que describen el acoplamiento de cuerdas como si fuera fijo se refieren generalmente al valor de expectativa de vacío . Esto es gratis para tener cualquier valor en la teoría bosónica donde no hay superpotencial .

Los operadores de creación y aniquilación son operadores matemáticos que tienen aplicaciones generalizadas en mecánica cuántica , especialmente en el estudio de osciladores de armónicos cuánticos y sistemas de muchas partículas. ^[1] Un operador de aniquilación reduce la cantidad de partículas en un estado dado en uno. Un operador de creación aumenta el número de partículas en un estado dado en uno, y es el adjunto del operador de aniquilación. En muchos subcampos de la física y la química , el uso de estos operadores en lugar de las funciones de onda se conoce como segunda cuantización .

Los operadores de creación y aniquilación pueden actuar sobre estados de varios tipos de partículas. Por ejemplo, en la química cuántica y la teoría de muchos cuerpos, los operadores de creación y aniquilación a menudo actúan sobre estados de electrones . También pueden referirse específicamente a los operadores de escalera para el oscilador armónico cuántico . En este último caso, el operador de subida se interpreta como un operador de creación, que agrega una cantidad de energía al sistema del oscilador (de manera similar para el operador que baja). Se pueden utilizar para representar fonones .

Las matemáticas para los operadores de creación y aniquilación para bosones son las mismas que para losoperadores de escalera del oscilador armónico cuántico . ^[2] Por ejemplo, el conmutador de los operadores de creación y aniquilación que están asociados con el mismo estado de bosón es igual a uno, mientras que todos los demás conmutadores desaparecen. Sin embargo, para los fermiones, las matemáticas son diferentes, e incluyen anticonmutadores en lugar de conmutadores.

Operadores de escalera para el oscilador armónico cuántico [ editar ]

Ver también: Oscilador armónico cuántico § Método del operador de escalera

En el contexto de la oscilador armónico cuántico , uno reinterpreta el operador escalera como operadores de creación y aniquilación, añadiendo o restando fijos quanta de energía para el sistema de oscilador.

Los operadores de creación / aniquilación son diferentes para los bosones (giro de entero) y los fermiones (giro de medio entero). Esto se debe a que sus funciones de onda tienen diferentes propiedades de simetría .

Primero considere el caso bosónico más simple de los fonones del oscilador armónico cuántico. Comience con la ecuación de Schrödinger para el oscilador armónico cuántico independiente de tiempo unidimensional ,

$${\ displaystyle \ left (- {\ frac {\ hbar ^ {2}} {2m}} {\ frac {d ^ {2}} {dx ^ {2}}} + {\ frac {1} {2} } m \ omega ^ {2} x ^ {2} \ derecha) \ psi (x) = E \ psi (x).}

Hacer una sustitución de coordenadas para no dimensionalizar la ecuación diferencial.

$${\ displaystyle x \ = \ {\ sqrt {\ frac {\ hbar} {m \ omega}}} q.}

La ecuación de Schrödinger para el oscilador se convierte en

$${\ displaystyle {\ frac {\ hbar \ omega} {2}} \ left (- {\ frac {d ^ {2}} {dq ^ {2}}} + q ^ {2} \ right) \ psi ( q) = E \ psi (q).}

Tenga en cuenta que la cantidad $${\ displaystyle \ hbar \ omega = h \ nu} es la misma energía que la que se encuentra para los cuantos de luz y que el paréntesis en el Hamiltoniano se puede escribir como

$${\ displaystyle - {\ frac {d ^ {2}} {dq ^ {2}}} + q ^ {2} = \ left (- {\ frac {d} {dq}} + q \ right) \ left ({\ frac {d} {dq}} + q \ right) + {\ frac {d} {dq}} qq {\ frac {d} {dq}}.}

Los dos últimos términos pueden simplificarse considerando su efecto en una función diferenciable arbitraria $${\ displaystyle f (q),}

$${\ displaystyle \ left ({\ frac {d} {dq}} qq {\ frac {d} {dq}} \ right) f (q) = {\ frac {d} {dq}} (qf (q) ) -q {\ frac {df (q)} {dq}} = f (q)}

lo que implica,

$${\ displaystyle {\ frac {d} {dq}} qq {\ frac {d} {dq}} = 1,}

Coincidiendo con la habitual relación canónica de conmutación. $${\ displaystyle -i [q, p] = 1}, en la posición del espacio de representación: $${\ displaystyle p: = - i {\ frac {d} {dq}}}.

Por lo tanto,

$${\ displaystyle - {\ frac {d ^ {2}} {dq ^ {2}}} + q ^ {2} = \ left (- {\ frac {d} {dq}} + q \ right) \ left ({\ frac {d} {dq}} + q \ derecha) +1}

y la ecuación de Schrödinger para el oscilador se convierte, con la sustitución de lo anterior y la reorganización del factor de 1/2,

$${\ displaystyle \ hbar \ omega \ left [{\ frac {1} {\ sqrt {2}}} \ left (- {\ frac {d} {dq}} + q \ right) {\ frac {1} { \ sqrt {2}}} \ left ({\ frac {d} {dq}} + q \ right) + {\ frac {1} {2}} \ right] \ psi (q) = E \ psi (q ).

Si se define

$${\ displaystyle a ^ {\ dagger} \ = \ {\ frac {1} {\ sqrt {2}}} \ left (- {\ frac {d} {dq}} + q \ right)}

como el "operador de creación" o el "operador de subida" y

$${\ displaystyle a \ \ = \ {\ frac {1} {\ sqrt {2}}} \ left (\ \ \ \! {\ frac {d} {dq}} + q \ right)}

como el "operador de aniquilación" o el "operador de descenso" , la ecuación de Schrödinger para el oscilador se reduce a

$${\ displaystyle \ hbar \ omega \ left (a ^ {\ dagger} a + {\ frac {1} {2}} \ right) \ psi (q) = E \ psi (q).}

Esto es significativamente más simple que la forma original. Las simplificaciones adicionales de esta ecuación le permiten a uno derivar todas las propiedades enumeradas anteriormente hasta ahora.

Dejando $${\ displaystyle p = -i {\ frac {d} {dq}}}, dónde $${\ displaystyle p} es el operador de momento no dimensionalizado que uno tiene

$${\ displaystyle [q, p] = i \,}

y

$${\ displaystyle a = {\ frac {1} {\ sqrt {2}}} (q + ip) = {\ frac {1} {\ sqrt {2}}} \ left (q + {\ frac {d} { dq}} \ derecha)}

$${\ displaystyle a ^ {\ dagger} = {\ frac {1} {\ sqrt {2}}} (q-ip) = {\ frac {1} {\ sqrt {2}}} \ left (q- { \ frac {d} {dq}} \ right).}

Tenga en cuenta que esto implica

$${\ displaystyle [a, a ^ {\ dagger}] = {\ frac {1} {2}} [q + ip, q-ip] = {\ frac {1} {2}} ([q, -ip ] + [ip, q]) = {\ frac {-i} {2}} ([q, p] + [q, p]) = 1.}

Los operadores $${\ displaystyle a \,} y $${\ displaystyle a ^ {\ dagger} \,} Se puede contrastar con los operadores normales , que conmutan con sus adjuntos. ^[4]

Utilizando las relaciones de conmutación indicadas anteriormente, el operador hamiltoniano puede expresarse como

$${\ displaystyle {\ hat {H}} = \ hbar \ omega \ left (a \, a ^ {\ dagger} - {\ frac {1} {2}} \ right) = \ hbar \ omega \ left (a ^ {\ dagger} \, a + {\ frac {1} {2}} \ right). \ qquad \ qquad (*)}

Uno puede calcular las relaciones de conmutación entre $${\ displaystyle a \,} y $${\ displaystyle a ^ {\ dagger} \,}Los operadores y el hamiltoniano: ^[5]

$${\ displaystyle [{\ hat {H}}, a] = [\ hbar \ omega \ left (aa ^ {\ dagger} - {\ frac {1} {2}} \ right), a] = \ hbar \ omega [aa ^ {\ dagger}, a] = \ hbar \ omega (a [a ^ {\ dagger}, a] + [a, a] a ^ {\ dagger}) = - \ hbar \ omega a.}

$${\ displaystyle [{\ hat {H}}, a ^ {\ dagger}] = \ hbar \ omega \, a ^ {\ dagger}.}

Estas relaciones pueden usarse para encontrar fácilmente todos los estados propios de energía del oscilador armónico cuántico de la siguiente manera.

Asumiendo que $${\ displaystyle \ psi _ {n}} es un estado propio del hamiltoniano $${\ displaystyle {\ hat {H}} \ psi _ {n} = E_ {n} \, \ psi _ {n}}. Usando estas relaciones de conmutación, se sigue que ^[5]

$${\ displaystyle {\ hat {H}} \, a \ psi _ {n} = (E_ {n} - \ hbar \ omega) \, a \ psi _ {n}.}

$${\ displaystyle {\ hat {H}} \, a ^ {\ dagger} \ psi _ {n} = (E_ {n} + \ hbar \ omega) \, a ^ {\ dagger} \ psi _ {n} .}

Esto muestra que $${\ displaystyle a \ psi _ {n}} y $${\ displaystyle a ^ {\ dagger} \ psi _ {n}} También son estados propios del hamiltoniano, con valores propios. $${\ displaystyle E_ {n} - \ hbar \ omega} y $${\ displaystyle E_ {n} + \ hbar \ omega}respectivamente. Esto identifica a los operadores.$${\ displaystyle a} y $${\ displaystyle a ^ {\ dagger}}como operadores de "reducción" y "elevación" entre estados propios adyacentes. La diferencia de energía entre estados propios adyacentes es $${\ displaystyle \ Delta E = \ hbar \ omega}.

El estado fundamental se puede encontrar asumiendo que el operador de bajada posee un núcleo no trivial: $${\ displaystyle a \, \ psi _ {0} = 0} con $${\ displaystyle \ psi _ {0} \ neq 0}. Aplicación de la fórmula anterior para los rendimientos hamiltonianos.

$${\ displaystyle 0 = \ hbar \ omega \, a ^ {\ dagger} a \ psi _ {0} = \ left ({\ hat {H}} - {\ frac {\ hbar \ omega} {2}} \ derecha) \, \ psi _ {0}.}

Asi que $${\ displaystyle \ psi _ {0}} Es una función propia del hamiltoniano.

Esto le da energía al estado fundamental. $${\ displaystyle E_ {0} = \ hbar \ omega / 2}, que permite identificar el valor propio de energía de cualquier estado propio $${\ displaystyle \ psi _ {n}}como ^[5]

$${\ displaystyle E_ {n} = \ left (n + {\ frac {1} {2}} \ right) \ hbar \ omega.}

Además, resulta que el primer operador mencionado en (*), el operador de número $${\ displaystyle N = a ^ {\ dagger} a \ ,,} Juega el papel más importante en las aplicaciones, mientras que el segundo, $${\ displaystyle aa ^ {\ dagger} \,} simplemente puede ser reemplazado por $${\ displaystyle N + 1}.

Por consiguiente,

$${\ displaystyle \ hbar \ omega \, \ left (N + {\ frac {1} {2}} \ right) \, \ psi (q) = E \, \ psi (q) ~.}

El operador de la evolución del tiempo es entonces

$${\ displaystyle U (t) = \ exp (-it {\ hat {H}} / \ hbar) = \ exp (-it \ omega (a ^ {\ dagger} a + 1/2)) ~,}

$${\ displaystyle = e ^ {- it \ omega / 2} ~ \ sum _ {k = 0} ^ {\ infty} {(e ^ {- i \ omega t} -1) ^ {k} \ sobre k! } a ^ {{\ dagger} {k}} a ^ {k} ~.}

Funciones propias explícitas [ editar ]

El estado fundamental $${\ displaystyle \ \ psi _ {0} (q)}del oscilador armónico cuántico se puede encontrar imponiendo la condición de que

$${\ displaystyle a \ \ psi _ {0} (q) = 0.}

Escrito como una ecuación diferencial, la función de onda satisface

$${\ displaystyle q \ psi _ {0} + {\ frac {d \ psi _ {0}} {dq}} = 0}

con la solución

$${\ displaystyle \ psi _ {0} (q) = C \ exp \ left (- {q ^ {2} \ over 2} \ right).}

La constante de normalización C se encuentra que es  $${\ displaystyle 1 / {\ sqrt [{4}] {\ pi}}}  desde $${\ displaystyle \ int _ {- \ infty} ^ {\ infty} \ psi _ {0} ^ {*} \ psi _ {0} \, dq = 1}, utilizando la integral gaussiana . Ahora se pueden encontrar fórmulas explícitas para todas las funciones propias mediante la aplicación repetida de$${\ displaystyle a ^ {\ dagger}} a $${\ displaystyle \ psi _ {0}}. ^[6]

Representación de la matriz [ editar ]

La expresión matricial de los operadores de creación y aniquilación del oscilador armónico cuántico con respecto a la base ortonormal anterior es

${\displaystyle a^{\dagger }={\begin{pmatrix}0&0&0&\dots &0&\dots \\{\sqrt {1}}&0&0&\dots &0&\dots \\0&{\sqrt {2}}&0&\dots &0&\dots \\0&0&{\sqrt {3}}&\dots &0&\dots \\\vdots &\vdots &\vdots &\ddots &\vdots &\dots \\0&0&0&\dots &{\sqrt {n}}&\dots &\\\vdots &\vdots &\vdots &\vdots &\vdots &\ddots \end{pmatrix}}}$

{\ displaystyle a = {\ begin {pmatrix} 0 & {\ sqrt {1}} & 0 & 0 & \ dots & 0 & \ dots \\ 0 & 0 & {\ sqrt {2}} & 0 & \ dots & 0 & \ dots \\ 0 & 0 & 0 & {\ sqrt {3} } & \ dots & 0 & \ dots \\ 0 & 0 & 0 & 0 & \ ddots & \ vdots & \ dots \\\ vdots & \ vdots & \ vdots & \ vdots & \ ddots & {\ sqrt {n}} & \ dots \\ 0 & 0 & 0 & 0 & \ dots & 0 & \ ddots \\\ vdots & \ vdots & \ vdots & \ vdots & \ vdots & \ vdots & \ ddots \ end {pmatrix}}}

Estos se pueden obtener a través de las relaciones. $${\ displaystyle a_ {ij} ^ {\ dagger} = \ langle \ psi _ {i} \ mid a ^ {\ dagger} \ mid \ psi _ {j} \ rangle} y $${\ displaystyle a_ {ij} = \ langle \ psi _ {i} \ mid a \ mid \ psi _ {j} \ rangle}. Los vectores propios$${\ displaystyle \ psi _ {i}} son las del oscilador armónico cuántico, ya veces se las denomina "base numérica".

Operadores de creación y aniquilación generalizados [ editar ]

Artículo principal: algas CCR y CAR

Los operadores derivados anteriormente son en realidad una instancia específica de una noción más generalizada de operadores de creación y aniquilación. La forma más abstracta de los operadores se construye de la siguiente manera. Dejar$${\ displaystyle H}ser un espacio de Hilbert de una partícula (es decir, cualquier espacio de Hilbert, visto como que representa el estado de una sola partícula).

El ( bosónico ) CCR álgebra sobre$${\ displaystyle H}es el álgebra con conjugación-operador (llamado * ) generado de forma abstracta por elementos$${\ displaystyle a (f)}, dónde $${\ displaystyle f \,}oscila libremente sobre $${\ displaystyle H}, sujeto a las relaciones

$${\ displaystyle [a (f), a (g)] = [a ^ {\ dagger} (f), a ^ {\ dagger} (g)] = 0}

$${\ displaystyle [a (f), a ^ {\ dagger} (g)] = \ langle f \ mid g \ rangle,}

en notación bra-ket .

El mapa $${\ displaystyle a: f \ to a (f)} desde $${\ displaystyle H}Se requiere que el álgebra CCR bosónica sea complejo antilineal (esto agrega más relaciones). Su adjunto es$${\ displaystyle a ^ {\ dagger} (f)}y el mapa $${\ displaystyle f \ to a ^ {\ dagger} (f)}es complejo lineal en h . Así$${\ displaystyle H}se integra como un subespacio vectorial complejo de su propio álgebra CCR. En una representación de este álgebra, el elemento.$${\ displaystyle a (f)} Se realizará como un operador de aniquilación, y $${\ displaystyle a ^ {\ dagger} (f)} Como operador de creación.

En general, el álgebra CCR es de dimensión infinita. Si tomamos un espacio de Banach completado, se convierte en un álgebra C * . El álgebra de CCR sobre$${\ displaystyle H}está estrechamente relacionado con, pero no idéntico, a un álgebra de Weyl .

Para los fermiones, el álgebra CAR (fermiónico) sobre$${\ displaystyle H}está construido de manera similar, pero usando anticonmutador relaciones de cambio, es decir,

$${\ displaystyle \ {a (f), a (g) \} = \ {a ^ {\ dagger} (f), a ^ {\ dagger} (g) \} = 0}

$${\ displaystyle \ {a (f), a ^ {\ dagger} (g) \} = \ langle f \ mid g \ rangle.}

El álgebra CAR es de dimensión finita solo si $${\ displaystyle H}es finito dimensional. Si tomamos un espacio de Banach completado (solo necesario en el caso de dimensión infinita), se convierte en un$${\ displaystyle C ^ {*}} álgebra. El álgebra CAR está estrechamente relacionado con, pero no es idéntico a, el álgebra de Clifford .

Físicamente hablando, $${\ displaystyle a (f)} elimina (es decir, aniquila) una partícula en el estado $${\ displaystyle | f \ rangle} mientras $${\ displaystyle a ^ {\ dagger} (f)} crea una partícula en el estado $${\ displaystyle | f \ rangle}.

El estado de vacío de campo libre es el estado | 0 $${\ displaystyle \ scriptstyle \ rangle} sin partículas, caracterizado por

$${\ displaystyle a (f) \ left | 0 \ right \ rangle = 0.}

Si $${\ displaystyle | f \ rangle} se normaliza para que $${\ displaystyle \ langle f | f \ rangle = 1}, entonces $${\ displaystyle N = a ^ {\ dagger} (f) a (f)} Da la cantidad de partículas en el estado. $${\ displaystyle | f \ rangle}.

Operadores de creación y aniquilación para ecuaciones de reacción-difusión [ editar ]

La descripción del operador de aniquilación y creación también ha sido útil para analizar ecuaciones de difusión de reacciones clásicas, como la situación en la que un gas de moléculas $${\ displaystyle A} Difundir e interactuar en contacto, formando un producto inerte: $${\ displaystyle A + A \ to \ emptyset}. Para ver cómo este tipo de reacción puede describirse mediante el formalismo del operador de aniquilación y creación, considere$${\ displaystyle n_ {i}}partículas en un sitio i en una red unidimensional. Cada partícula se mueve hacia la derecha o hacia la izquierda con una cierta probabilidad, y cada par de partículas en el mismo sitio se aniquila entre sí con una cierta otra probabilidad.

La probabilidad de que una partícula abandone el sitio durante el corto período de tiempo dt es proporcional a$${\ displaystyle n_ {i} \, dt}, digamos una probabilidad $${\ displaystyle \ alpha n_ {i} dt} para saltar a la izquierda y $${\ displaystyle \ alpha n_ {i} \, dt}para saltar a la derecha. Todos$${\ displaystyle n_ {i}} Las partículas se mantendrán puestas con una probabilidad. $${\ displaystyle 1-2 \ alpha n_ {i} \, dt}. (Dado que dt es tan corto, la probabilidad de que dos o más salgan durante dt es muy pequeña y se ignorará).

Ahora podemos describir la ocupación de partículas en la red como un 'ket' de la forma

$${\ displaystyle | \ dots, n _ {- 1}, n_ {0}, n_ {1}, \ dots \ rangle}. Representa la yuxtaposición (o conjunción, o producto tensorial) de los estados numéricos. $${\ displaystyle \ dots, | n _ {- 1} \ rangle} $${\ displaystyle | n_ {0} \ rangle}, $${\ displaystyle | n_ {1} \ rangle, \ dots}Ubicados en los sitios individuales de la celosía. Recordar

$${\ displaystyle a \ mid \! n \ rangle = {\ sqrt {n}} \ | n-1 \ rangle}

$${\ displaystyle a ^ {\ dagger}}y

$${\ displaystyle a ^ {\ dagger} \ mid \! n \ rangle = {\ sqrt {n + 1}} \ mid n + 1 \ rangle,}

para todos n  ≥ 0, mientras que

$${\ displaystyle [a, a ^ {\ dagger}] = 1}

Esta definición de los operadores ahora se cambiará para adaptarse a la naturaleza "no cuántica" de este problema y usaremos la siguiente definición:

$${\ displaystyle a \ mid \! n \ rangle = n \ | n-1 \ rangle}

$${\ displaystyle a ^ {\ dagger} \ mid \! n \ rangle = \ \ mid n + 1 \ rangle}

tenga en cuenta que aunque el comportamiento de los operadores en los kets se ha modificado, estos operadores siguen obedeciendo la relación de conmutación

$${\ displaystyle [a, a ^ {\ dagger}] = 1}

Ahora define $${\ displaystyle a_ {i}} para que se aplique $${\ displaystyle a} a $${\ displaystyle | n_ {i} \ rangle}. Correspondientemente, definir $${\ displaystyle a_ {i} ^ {\ dagger}} como aplicando $${\ displaystyle a ^ {\ dagger}} a $${\ displaystyle | n_ {i} \ rangle}. Así, por ejemplo, el efecto neto de $${\ displaystyle a_ {i-1} a_ {i} ^ {\ dagger}} es mover una partícula de la $${\ displaystyle i ^ {\ text {th}}} al $${\ displaystyle (i-1) ^ {\ text {th}}}sitio mientras se multiplica con el factor apropiado.

Esto permite escribir el comportamiento difuso puro de las partículas como

$${\ displaystyle \ parcial _ {t} \ mid \! \ psi \ rangle = - \ alpha \ sum (2a_ {i} ^ {\ dagger} a_ {i} -a_ {i-1} ^ {\ dagger} a_ {i} -a_ {i + 1} ^ {\ dagger} a_ {i}) \ mid \! \ psi \ rangle = - \ alpha \ sum (a_ {i} ^ {\ dagger} -a_ {i-1 } ^ {\ dagger}) (a_ {i} -a_ {i-1}) \ mid \! \ psi \ rangle,}

donde la suma ha terminado $${\ displaystyle i}.

El término de reacción se puede deducir notando que $${\ displaystyle n} las partículas pueden interactuar en $${\ displaystyle n (n-1)} diferentes maneras, por lo que la probabilidad de que un par aniquila es $${\ displaystyle \ lambda n (n-1) dt}, dando un término

$${\ displaystyle \ lambda \ sum (a_ {i} a_ {i} -a_ {i} ^ {\ dagger} a_ {i} ^ {\ dagger} a_ {i} a_ {i})}

donde el estado número n se reemplaza por el estado número n  - 2 en el sitio$${\ displaystyle i} a una cierta velocidad.

Así el estado evoluciona por

$${\ displaystyle \ parcial _ {t} \ mid \! \ psi \ rangle = - \ alpha \ sum (a_ {i} ^ {\ dagger} -a_ {i-1} ^ {\ dagger}) (a_ {i } -a_ {i-1}) \ mid \! \ psi \ rangle + \ lambda \ sum (a_ {i} ^ {2} -a_ {i} ^ {\ dagger 2} a_ {i} ^ {2} ) \ mid \! \ psi \ rangle}

Se pueden incluir otros tipos de interacciones de manera similar.

Este tipo de notación permite el uso de técnicas de teoría de campos cuánticos para el análisis de sistemas de difusión de reacciones.

Operadores de creación y aniquilación en teorías de campos cuánticos [ editar ]

Artículos principales: Segunda cuantización y Teoría cuántica de campos § Segunda cuantización

En las teorías de campo cuántico y los problemas de muchos cuerpos, se trabaja con operadores de creación y aniquilación de estados cuánticos.$${\ displaystyle a_ {i} ^ {\ dagger}} y $${\ displaystyle a_ {i} ^ {\,}}. Estos operadores cambian los valores propios del operador de número ,

$${\ displaystyle N = \ sum _ {i} n_ {i} = \ sum _ {i} a_ {i} ^ {\ dagger} a_ {i} ^ {\,}},

Por uno, en analogía con el oscilador armónico. Los índices (tales como$${\ displaystyle i}) representan números cuánticos que etiquetan los estados de una sola partícula del sistema; Por lo tanto, no son necesariamente números únicos. Por ejemplo, una tupla de números cuánticos.$${\ displaystyle (n, l, m, s)}Se utiliza para etiquetar estados en el átomo de hidrógeno .

Las relaciones de conmutación de los operadores de creación y aniquilación en un sistema de bosones múltiples son,

$${\ displaystyle [a_ {i} ^ {\,}, a_ {j} ^ {\ dagger}] \ equiv a_ {i} ^ {\,} a_ {j} ^ {\ dagger} -a_ {j} ^ {\ dagger} a_ {i} ^ {\,} = \ delta _ {ij},}

$${\ displaystyle [a_ {i} ^ {\ dagger}, a_ {j} ^ {\ dagger}] = [a_ {i} ^ {\,}, a_ {j} ^ {\,}] = 0,}

dónde $${\ displaystyle [\ \, \ \]}es el conmutador y$${\ displaystyle \ delta _ {ij}}es el delta de Kronecker .

Para los fermiones , el conmutador es reemplazado por el anticonmutador. $${\ displaystyle \ {\ \, \ \ \}},

$${\ displaystyle \ {a_ {i} ^ {\,}, a_ {j} ^ {\ dagger} \} \ equiv a_ {i} ^ {\,} a_ {j} ^ {\ dagger} + a_ {j } ^ {\ dagger} a_ {i} ^ {\,} = \ delta _ {ij},}

$${\ displaystyle \ {a_ {i} ^ {\ dagger}, a_ {j} ^ {\ dagger} \} = \ {a_ {i} ^ {\,}, a_ {j} ^ {\,} \} = 0.}

Por lo tanto, intercambiando desunión (es decir, $${\ displaystyle i \ neq j}) los operadores en un producto de creación o aniquilación los operadores revertirán el signo en los sistemas de fermión, pero no en los sistemas de bosones.

Si los estados etiquetados por i son una base ortonormal de un espacio H de Hilbert , entonces el resultado de esta construcción coincide con la construcción del álgebra CCR y del álgebra CAR en la sección anterior, pero una. Si representan "vectores propios" correspondientes al espectro continuo de algún operador, como para las partículas no unidas en QFT, entonces la interpretación es más sutil.